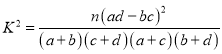ЬтФПФкШн
ЁОЬтФПЁПФГГЇИљОнЪаГЁашЧѓПЊЗЂШ§НЧЛЈРКжЇМмЃЈШчЭМЃЉЃЌЩЯУцЮЊЛЈРКЃЌжЇМмгЩШ§ИљЯИИжЙмзщГЩЃЌПМТЧЕНИжЙмЕФЪмСІКЭЛЈРКжЪСПЕШвђЫиЃЌЩшМЦжЇМмгІТњзуЃКЂйШ§ИљЯИИжЙмГЄОљЮЊ1УзЃЈДжЯИКіТдВЛМЦЃЉЃЌЧвгыЕиУцЫљГЩЕФНЧОљЮЊ![]() ЃЛЂкМмУцгыМмЕзЦНааЃЌЧвМмУцШ§НЧаЮ
ЃЛЂкМмУцгыМмЕзЦНааЃЌЧвМмУцШ§НЧаЮ![]() гыМмЕзШ§НЧаЮ
гыМмЕзШ§НЧаЮ![]() ОљЮЊЕШБпШ§НЧаЮЃЛЂлШ§ИљЯИИжЙмЯрНЛДІЕФНкЕу
ОљЮЊЕШБпШ§НЧаЮЃЛЂлШ§ИљЯИИжЙмЯрНЛДІЕФНкЕу![]() ЗжШ§ИљЯИИжЙмЩЯЁЂЯТСНЖЮжЎБШОљЮЊ
ЗжШ§ИљЯИИжЙмЩЯЁЂЯТСНЖЮжЎБШОљЮЊ![]() .ЖЈвхЃКМмУцгыМмЕзЕФОрРыЮЊЁАжЇМмИпЖШЁБЃЌМмЕзШ§НЧаЮ
.ЖЈвхЃКМмУцгыМмЕзЕФОрРыЮЊЁАжЇМмИпЖШЁБЃЌМмЕзШ§НЧаЮ![]() ЕФУцЛ§гыЁАжЇМмИпЖШЁБЕФГЫЛ§ЮЊЁАжЇМмашвЊПеМфЁБ.
ЕФУцЛ§гыЁАжЇМмИпЖШЁБЕФГЫЛ§ЮЊЁАжЇМмашвЊПеМфЁБ.
ЃЈ1ЃЉЕБ![]() ЪБЃЌЧѓЁАжЇМмИпЖШЁБЃЛ
ЪБЃЌЧѓЁАжЇМмИпЖШЁБЃЛ
ЃЈ2ЃЉЧѓЁАжЇМмашвЊПеМфЁБЕФзюДѓжЕ.
ЁОД№АИЁПЃЈ1ЃЉ![]() Уз.ЃЈ2ЃЉ
Уз.ЃЈ2ЃЉ![]() СЂЗНУз.
СЂЗНУз.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬтвт![]() гыЕиУцЫљГЩЕФНЧЮЊ
гыЕиУцЫљГЩЕФНЧЮЊ![]() ЃЌ
ЃЌ![]() УзЃЌДгЖј
УзЃЌДгЖј![]() .
.
ЃЈ2ЃЉЙ§![]() зї
зї![]() ЦНУц
ЦНУц![]() ЃЌДЙзуЮЊ
ЃЌДЙзуЮЊ![]() ЃЌЧв
ЃЌЧв![]() ЃЌБэЪОГі
ЃЌБэЪОГі![]() ЃЌНјЖј
ЃЌНјЖј![]() ЃЌ
ЃЌ![]() ЃЌСю
ЃЌСю![]() ЃЌРћгУЕМЪ§МДПЩЧѓНт.
ЃЌРћгУЕМЪ§МДПЩЧѓНт.
НтЃКЃЈ1ЃЉвђЮЊМмУцгыМмЕзЦНааЃЌЧв![]() гыЕиУцЫљГЩЕФНЧЮЊ
гыЕиУцЫљГЩЕФНЧЮЊ![]() ЃЌ
ЃЌ![]() УзЃЌ
УзЃЌ
ЫљвдЁАжЇМмИпЖШЁБ![]() ЃЈУзЃЉ.
ЃЈУзЃЉ.
ЃЈ2ЃЉЙ§![]() зї
зї![]() ЦНУц
ЦНУц![]() ЃЌДЙзуЮЊ
ЃЌДЙзуЮЊ![]() .
.
гж![]() ЦНУц
ЦНУц![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌ
ЃЌ
гж![]() гыЕиУцЫљГЩЕФНЧЮЊ
гыЕиУцЫљГЩЕФНЧЮЊ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌ
ЃЌ
ЭЌРэ![]() ЃЌ
ЃЌ
Ыљвд![]() ЮЊЕШБпШ§НЧаЮ
ЮЊЕШБпШ§НЧаЮ![]() ЭтаФЃЌвВЮЊЦфжиаФЃЌ
ЭтаФЃЌвВЮЊЦфжиаФЃЌ
Ыљвд![]() ЃЌ
ЃЌ
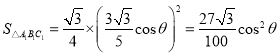 ЃЌ
ЃЌ
МЧЁАжЇМмашвЊПеМфЁБЮЊ![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ![]() .
.
Сю![]() ЃЌдђ
ЃЌдђ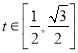 .
.
Ыљвд![]() ЃЌ
ЃЌ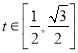 .
.
гж![]()
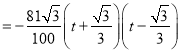 ЃЌ
ЃЌ
дђЕБ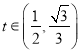 ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ![]() ЕЅЕїЕндіЃЛЕБ
ЕЅЕїЕндіЃЛЕБ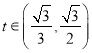 ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ![]() ЕЅЕїЕнМѕ.
ЕЅЕїЕнМѕ.
ЫљвдЕБ![]() ЪБЃЌ
ЪБЃЌ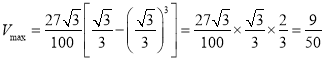 ЃЈСЂЗНУзЃЉ.
ЃЈСЂЗНУзЃЉ.
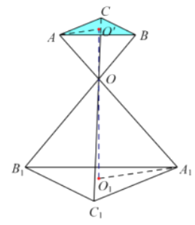
Д№ЃКЃЈ1ЃЉЕБ![]() ЪБЃЌЁАжЇМмИпЖШЁБЮЊ
ЪБЃЌЁАжЇМмИпЖШЁБЮЊ![]() УзЃЛ
УзЃЛ
ЃЈ2ЃЉЁАжЇМмашвЊПеМфЁБЕФзюДѓжЕЮЊ![]() СЂЗНУз.
СЂЗНУз.