题目内容
12.已知函数f(x)=$\sqrt{3}sin?x$+cos(?x+$\frac{π}{3}$)+cos(?x$-\frac{π}{3}$),x∈R,?>0.若函数f(x)的最小正周期为π,(1)求函数f(x)在区间$[{-\frac{π}{4},\frac{π}{4}}]$上的值域;
(2)则当x$∈[0,\frac{π}{2}]$时,求f(x)的单调递减区间.
分析 (1)由条件利用两角和差的正弦、余弦公式化简f(x)的解析式,再利用正弦函数的定义域和值域求得函数f(x)在区间$[{-\frac{π}{4},\frac{π}{4}}]$上的值域.
(2)利用正弦函数的减区间求得当x$∈[0,\frac{π}{2}]$时,f(x)的单调递减区间.
解答 解:(1)f(x)=$\sqrt{3}$sin?x+cos?x=2sin(?x+$\frac{π}{6}$)∵T=$\frac{2π}{ω}$=π,∴ω=2.
在区间$[{-\frac{π}{4},\frac{π}{4}}]$上,2x+$\frac{π}{6}$∈[-$\frac{π}{3}$,$\frac{2π}{3}$],f(x)=2sin(2x+$\frac{π}{6}$)∈[-$\sqrt{3}$,2].
(2)令2kπ+$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$,求得kπ+$\frac{π}{6}$≤x≤kπ+$\frac{2π}{3}$,故函数的减区间为[kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$],k∈Z.
再根据x∈[0,$\frac{π}{2}$],可得函数的减区间为$[\frac{π}{6},\frac{π}{2}]$.
点评 本题主要考查两角和差的正弦、余弦公式,正弦函数的定义域和值域,正弦函数的减区间,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.设x∈R,则“l<x<2”是“l<x<3”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
3.函数f(x)=ex+x-2的零点所在的区间是(e≈2.71828)( )
| A. | (0,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,1) | C. | (1,2) | D. | (2,3) |
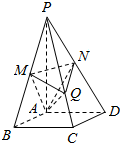 如图,在四棱锥P-ABCD中,底面是边长为2$\sqrt{3}$的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=2$\sqrt{6}$,M,N分别为PB,PD的中点.
如图,在四棱锥P-ABCD中,底面是边长为2$\sqrt{3}$的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=2$\sqrt{6}$,M,N分别为PB,PD的中点.