题目内容
【题目】如图,多面体 ABCDEF中,四边形ABCD是边长为2的菱形,且平面ABCD⊥平面DCE.AF∥DE,且AF=![]() DE=2,BF=2
DE=2,BF=2![]() .
.
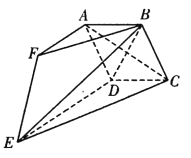
(1)求证:AC⊥BE;
(2)若点F到平面DCE的距离为![]() ,求直线EC与平面BDE所成角的正弦值.
,求直线EC与平面BDE所成角的正弦值.
【答案】(1)见解析;
(2)![]() .
.
【解析】
(1)由题意及勾股数可证得平面![]() 平面
平面![]() ,再由面面垂直的性质可证DE与平面ABCD垂直,可得AC⊥DE,再结合菱形中的垂直证得
,再由面面垂直的性质可证DE与平面ABCD垂直,可得AC⊥DE,再结合菱形中的垂直证得![]() 平面
平面![]() ,从而得到结论;
,从而得到结论;
(2)设![]() ,连接
,连接![]() .由(1)
.由(1)![]() 平面
平面![]() ,则
,则![]() 是
是![]() 在平面
在平面![]() 内的射影,可得
内的射影,可得![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .由点F到平面DCE的距离可得菱形
.由点F到平面DCE的距离可得菱形![]() 中,
中,![]() ,可求得OC,在
,可求得OC,在![]() 中,可求得EC,则可得结果.
中,可求得EC,则可得结果.
(1)∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∵平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴AC⊥DE.①
∵四边形![]() 为菱形,
为菱形,
∴![]() . ②
. ②
由①②,且![]() ,
,
∴![]() 平面
平面![]() .
.
∴![]() .
.
(2)设![]() ,连接
,连接![]() .
.
由(1)![]() 平面
平面![]() ,∴
,∴![]() 是
是![]() 在平面
在平面![]() 内的射影,
内的射影,
∴![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.

∵![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离.
的距离.
在平面![]() 内作
内作![]() ,交
,交![]() 延长线于
延长线于![]() .
.
∵平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() .(或转化为点
.(或转化为点![]() 到平面
到平面![]() 的距离)
的距离)
∵![]() ,∴
,∴![]() ,
,
∴菱形![]() 中,
中,![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
∴![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

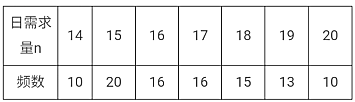
【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等级如表:
质量指标值m | 25≤m<35 | 15≤m<25或35≤m<45 | 0<m<15或45≤m≤65 |
等级 | 一等品 | 二等品 | 三等品 |
某企业从生产的这种产品中抽取100件产品作为样本,检测其质量指标值,得到如图所示的频率分布直方图.(同一组数据用该区间的中点值作代表):
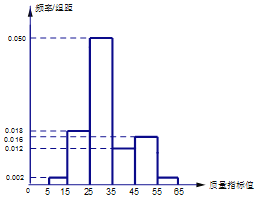
(1)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品82%”的规定?
(2)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值X近似满足X~N(31,122),则“质量提升月”活动后的质量指标值的均值比活动前大约提升或降低多少?
(3)若企业每件一等品售价180元,每件二等品售价150元,每件三等品售价120元,以样本中的频率代替相应概率,现有一名顾客随机购买两件产品,设其支付的费用为X(单位:元),求X的分布列及数学期望.