题目内容
【题目】某种产品的质量以其质量指标值衡量，并依据质量指标值划分等级如表：
质量指标值m | 25≤m＜35 | 15≤m＜25或35≤m＜45 | 0＜m＜15或45≤m≤65 |
等级 | 一等品 | 二等品 | 三等品 |
某企业从生产的这种产品中抽取100件产品作为样本，检测其质量指标值，得到如图所示的频率分布直方图．（同一组数据用该区间的中点值作代表）：
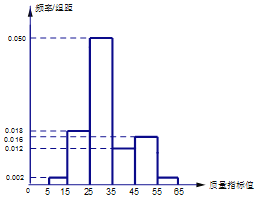
（1）根据以上抽样调查数据，能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品82%”的规定？
（2）该企业为提高产品质量，开展了“质量提升月”活动，活动后再抽样检测，产品质量指标值X近似满足X～N（31，122），则“质量提升月”活动后的质量指标值的均值比活动前大约提升或降低多少？
（3）若企业每件一等品售价180元，每件二等品售价150元，每件三等品售价120元，以样本中的频率代替相应概率，现有一名顾客随机购买两件产品，设其支付的费用为X（单位：元），求X的分布列及数学期望．
【答案】（1）不能认为这种产品符合规定；（2）降低了1.8；（3）见解析
【解析】
（1）根据抽样调查数据，可求得样本中一等品和二等品共有
件，进而可得到结论；
（2）由频率分布直方图，利用公式求得活动前样本的均值为
，即可作出比较，得到结论；
（3）由样品估计总体，可得一等品的概率为
，二等品的概率为
，三等品的概率为
，得到随机变量X的所有可能取值，利用概率的乘法公式，求得取每个值的概率，得到分布列，利用公式即可求得数学期望．
（1）根据抽样调查数据知，样本中一等品和二等品共有：（0.5+0.18+0.12）×100=80（件）
在样本中所占比例为80%，因此不能认为这种产品符合规定.
（2）由频率分布直方图知，活动前样本的均值为0.02×10+0.18×20+0.50×30+0.12×40+0.16×50+0.02×60=32.8，
又由活动后的均值为31，所以均值降低了1.8；
（3）由样品估计总体知，企业随机抽取一件产品为一等品的概率为，二等品的概率为，
三等品的概率为，随机变量X的所有可能取值为240，270，300，330，360．
，
，
．
所以X的分布列为：
X | 240 | 270 | 300 | 330 | 360 |
P（X） |
|
|
|
|
|
随机变量X的数学期望
．
