题目内容
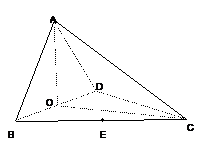 (本题满分14分)如图,四面体ABCD中,O、E分别是BD、BC的中点,
(本题满分14分)如图,四面体ABCD中,O、E分别是BD、BC的中点,
![]()
(I)求证:![]() 平面BCD;
平面BCD;
(II)求异面直线AB与CD所成角的余弦;
(III)求点E到平面ACD的距离.
(Ⅰ) 略(Ⅱ) ![]() (Ⅲ)
(Ⅲ)![]()
解析:
:方法一:
(I)证明:连结OC
![]() ………1分
………1分
![]()
 在
在![]() 中,由已知可得
中,由已知可得![]()
而![]()
![]()
![]() 即
即![]() ……………3分
……………3分
又![]()
![]() 平面
平面![]() ……………5分
……………5分
(II)解:取AC的中点M,连结OM、ME、OE,由E为BC的中点知![]()
![]() 直线OE与EM所成的锐角就是异面直线AB与CD所成的角。……………6分
直线OE与EM所成的锐角就是异面直线AB与CD所成的角。……………6分
在![]() 中,
中,
![]() ……………7分
……………7分
![]() 是直角
是直角![]() 斜边AC上的中线,
斜边AC上的中线,
![]() ……………8分
……………8分
![]()
![]() 异面直线AB与CD所成角大小的余弦为
异面直线AB与CD所成角大小的余弦为![]() ;……………9分
;……………9分
(III)解:设点E到平面ACD的距离为![]()
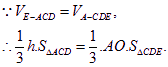 ……………11分
……………11分
在![]() 中,
中,![]()
![]() ……………12分
……………12分
而![]() ……………13分
……………13分

![]() 点E到平面ACD的距离为
点E到平面ACD的距离为![]() ……………14分
……………14分
方法二:
(I)同方法一.……………5分
(II)解:以O为原点,如图建立空间直角坐标系,
 则
则![]()
![]() ………………6分
………………6分
![]() …………7分
…………7分
 ………9分
………9分
![]() 异面直线AB与CD所成角大小的余弦为
异面直线AB与CD所成角大小的余弦为![]() ;……………10分
;……………10分
(III)解:设平面ACD的法向量为![]() 则
则
 …11分
…11分 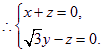
令![]() 得
得![]() 是平面ACD的一个法向量.……12分
是平面ACD的一个法向量.……12分
又![]()
![]() 点E到平面ACD的距离
点E到平面ACD的距离 ……14分
……14分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
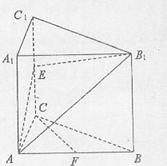

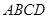 、
、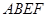 的边长都是1,平面
的边长都是1,平面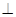 平面
平面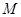 在
在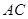 上移动,点
上移动,点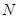 在
在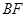 上移动,若
上移动,若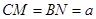 (
(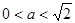 )
)
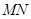 的长;
的长;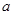 为何值时,
为何值时,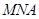 与面
与面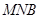 所成锐二面角余弦值的大小.
所成锐二面角余弦值的大小.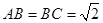 ,又E、F分别是C1A和C1B的中点。
,又E、F分别是C1A和C1B的中点。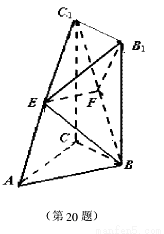 (1)求证:EF//平面ABC;
(1)求证:EF//平面ABC;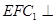 平面C1CBB1;
平面C1CBB1;