题目内容
【题目】已知抛物线![]() 的焦点为F,点P为抛物线C上一点,
的焦点为F,点P为抛物线C上一点,![]() ,O为坐标原点,
,O为坐标原点,![]() .
.
(1)求抛物线C的方程;
(2)设Q为抛物线C的准线上一点,过点F且垂直于OQ的直线交抛物线C于A,B两点记![]() ,
,![]() 的面积分别为
的面积分别为![]()
![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)根据![]() 可知直线
可知直线![]() 的倾斜角为
的倾斜角为![]() ,再利用几何关系求得
,再利用几何关系求得![]() ,代入抛物线方程化简即可.
,代入抛物线方程化简即可.
(2)设直线![]() 的方程为
的方程为![]() ,再分别计算
,再分别计算![]()
![]() 关于
关于![]() 的表达式,进而求得
的表达式,进而求得![]() 关于
关于![]() 的表达式再求范围即可.
的表达式再求范围即可.
解:(1)由题可知,直线![]() 的倾斜角为
的倾斜角为![]() ,故
,故![]() ,
,
代入方程可得![]() ,化简得
,化简得![]() ,因为
,因为![]() 所以
所以![]()
故抛物线C的方程为![]()
(2)显然直线![]() 斜率不为0,故设直线
斜率不为0,故设直线![]() 的方程为
的方程为![]() ,
,
联立 .设
.设![]() .则
.则![]() ,
,![]() .所以
.所以![]()
设![]() 则因为直线
则因为直线![]() 垂直于OQ.故
垂直于OQ.故![]() .所以
.所以![]()
又![]() 到直线
到直线![]() :
:![]() 的距离
的距离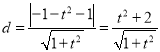 .
.
故![]() .
.
故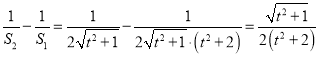 .
.
设![]() ,则
,则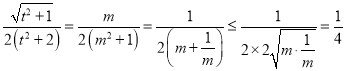
当且仅当![]() 即
即![]() 时取等号.又
时取等号.又![]() ,
,
所以![]() .
.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
【题目】某校高一年级有甲,乙,丙三位学生,他们前三次月考的物理成绩如表:
第一次月考物理成绩 | 第二次月考物理成绩 | 第三次月考物理成绩 | |
学生甲 | 80 | 85 | 90 |
学生乙 | 81 | 83 | 85 |
学生丙 | 90 | 86 | 82 |
则下列结论正确的是( )
A. 甲,乙,丙第三次月考物理成绩的平均数为86
B. 在这三次月考物理成绩中,甲的成绩平均分最高
C. 在这三次月考物理成绩中,乙的成绩最稳定
D. 在这三次月考物理成绩中,丙的成绩方差最大