题目内容
某公司有价值a万元的一条流水线,要提高该流水线的生产能力,就要对其进行技术改造,从而提高产品附加值,改造需要投入,假设附加值y万元与技术改造投入x万元之间的关系满足:①y与2a-x和x-a的乘积成正比;②
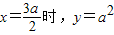 ;③y>0.
;③y>0.(I)设y=f(x),求f(x)表达式,并求y=f(x)的定义域;
(II)求每万元技术改造投入所获得的平均附加值的最大值,并求出此时的技术改造投入.
【答案】分析:(I)设y=k(2a-x)(x-a),利用当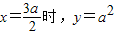 ,可求k=4,从而可得函数表达式,即可求得y=f(x)的定义域;
,可求k=4,从而可得函数表达式,即可求得y=f(x)的定义域;
(II)确定每万元技术改造投入函数解析式,利用基本不等式,即可求得结论.
解答:解:(I)设y=k(2a-x)(x-a),
因为当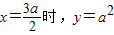 ,所以k=4
,所以k=4
所以y=4(2a-x)(x-a)
因为4(2a-x)(x-a)>0,所以a<x<2a
所以定义域为(a,2a);
(II) =-4(x+
=-4(x+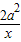 )+12a≤-4•2
)+12a≤-4•2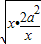 +12a=
+12a=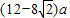
当且仅当x=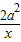 ,即x=
,即x= a时,每万元技术改造投入所获得的平均附加值的最大.
a时,每万元技术改造投入所获得的平均附加值的最大.
点评:本题考查函数解析式的确定,考查基本不等式的运用,考查学生的计算能力,属于中档题.
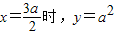 ,可求k=4,从而可得函数表达式,即可求得y=f(x)的定义域;
,可求k=4,从而可得函数表达式,即可求得y=f(x)的定义域;(II)确定每万元技术改造投入函数解析式,利用基本不等式,即可求得结论.
解答:解:(I)设y=k(2a-x)(x-a),
因为当
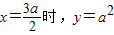 ,所以k=4
,所以k=4所以y=4(2a-x)(x-a)
因为4(2a-x)(x-a)>0,所以a<x<2a
所以定义域为(a,2a);
(II)
 =-4(x+
=-4(x+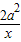 )+12a≤-4•2
)+12a≤-4•2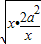 +12a=
+12a=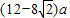
当且仅当x=
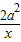 ,即x=
,即x= a时,每万元技术改造投入所获得的平均附加值的最大.
a时,每万元技术改造投入所获得的平均附加值的最大.点评:本题考查函数解析式的确定,考查基本不等式的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
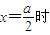 y=a2;
y=a2;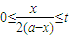 其中t为常数,且t∈[0,1].
其中t为常数,且t∈[0,1].