题目内容
设函数f(x)=sin(ωx+φ) (ω>0,-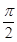 < φ<
< φ<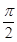 ),给出以下四个论断:
),给出以下四个论断:
①它的周期为π;
②它的图象关于直线x=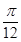 对称;
对称;
③它的图象关于点(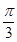 ,0)对称; ④在区间(-
,0)对称; ④在区间(-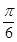 ,0)上是增函数.
,0)上是增函数.
以其中两个论断为条件,另两个论断作结论,写出你认为正确的一个命题:
__________________________(注:填上你认为正确的一种答案即可).
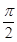 < φ<
< φ<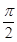 ),给出以下四个论断:
),给出以下四个论断:①它的周期为π;
②它的图象关于直线x=
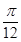 对称;
对称;③它的图象关于点(
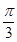 ,0)对称; ④在区间(-
,0)对称; ④在区间(-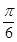 ,0)上是增函数.
,0)上是增函数.以其中两个论断为条件,另两个论断作结论,写出你认为正确的一个命题:
__________________________(注:填上你认为正确的一种答案即可).
①②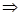 ③④(或①③
③④(或①③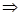 ②④)
②④)
 ③④(或①③
③④(或①③ ②④)
②④)解:①③⇒②④
由①知ω=2
∴f(x)=sin(2x+ϕ)(ω>0,-π/2<ϕ<π/2)
又由③,2×π/12+φ=kπ+π/2
∴φ=kπ+π3
又∵-π/2<ϕ<π/2
∴φ=π/3
∴f(x)=sin(2x+π/3)
∵2kπ-π/2≤2x+π/3≤2kπ+π/2
∴kπ-5π/12≤x≤kπ+π/12
∵[-π/6,0]⊆[-5π/12,π/12]
∴f(x)在区间[-π/6,0]上是增函数

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目

 时,求其最值及相应的
时,求其最值及相应的 值;
值; 的解集。
的解集。 ,
,
 的最大值和最小正周期;
的最大值和最小正周期; 的内角
的内角 的对边分别
的对边分别 且
且 ,
, ,若
,若 ,求
,求 的值.
的值.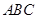 中,已知
中,已知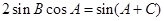 .
.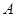 ;
;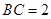 ,△
,△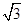 ,求
,求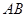 .
. sin C.
sin C.  ,若
,若 为第二象限角,求
为第二象限角,求
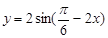 为增函数的区间是( )
为增函数的区间是( )
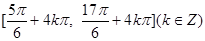

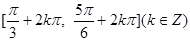
 ,则
,则 .
.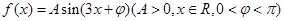 在
在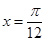 时取得最大值4.
时取得最大值4. 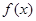 的最小正周期;
的最小正周期;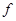 (
(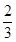 α +
α +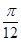 )=
)=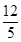 ,求sinα.
,求sinα.