题目内容
已知全集U=R,A={x|2≤x<5},集合B是函数y=
+lg(9-x)的定义域,
(1)求?UA∪B;
(2)求A∩(?UA∪B).
| 1 | ||
|
(1)求?UA∪B;
(2)求A∩(?UA∪B).
分析:(1)通过求函数y=
+lg(9-x)的定义域化简集合B,然后直接利用交集运算求解;
(2)直接利用交集运算求解.
| 1 | ||
|
(2)直接利用交集运算求解.
解答:解:要使函数y=
+lg(9-x)有意义,则
,解之得3<x<9.
∴B={x|3<x<9}.
(1)∵A={x|2≤x<5},B={x|3<x<9},
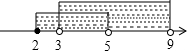
∴A∪B={x|2≤x<9},
又U=R,∴?UA∪B={x<2或x≥9};
(2)∵A={x|2≤x<5},?UA∪B={x<2或x≥9},
∴A∩(?UA∪B)=∅.
| 1 | ||
|
|
∴B={x|3<x<9}.
(1)∵A={x|2≤x<5},B={x|3<x<9},

∴A∪B={x|2≤x<9},
又U=R,∴?UA∪B={x<2或x≥9};
(2)∵A={x|2≤x<5},?UA∪B={x<2或x≥9},
∴A∩(?UA∪B)=∅.
点评:本题考查了对数函数的定义域的求法,考查了补集和交集的运算,是基础题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目