题目内容
如图,在直棱柱ABC—A1B1C1中,AC=BC=2,∠ACB=90º,AA1=2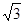 ,E,F分别为AB、CB中点,过直线EF作棱柱的截面,若截面与平面ABC所成的二面角的大小为60º,则截面的面积为( ).
,E,F分别为AB、CB中点,过直线EF作棱柱的截面,若截面与平面ABC所成的二面角的大小为60º,则截面的面积为( ).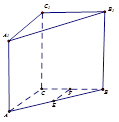
A.3或1 B.1 C.4或1 D.3或4
A
解析试题分析:根据截面与平面ABC所成的二面角的大小为60°,故需要分类讨论,利用截面为梯形,可以计算各边长,从而可求截面的面积.解:解:由题意,分类讨论:如右图,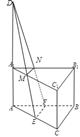
截面为MNFE,延长EM,CN,AA1,交于点D,∵直棱柱ABC-A1B1C1中,∠ACB=90°,E、F分别是AC、AB的中点,∴DE⊥EF,∴∠AED为截面与平面ABC所成的二面角,∴∠AED=60°,∵AE= AC=1,∴DE=2∵EF=
AC=1,∴DE=2∵EF=
BC=1∴S△DEF= ×2×1=1,∵DA=6
×2×1=1,∵DA=6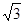 ,∴DA1=
,∴DA1= DA∴SDMN=
DA∴SDMN=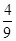 S△DEF=
S△DEF=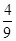 ,∴截面的面积为1
,∴截面的面积为1
设截面EFN'M'在底面中的射影为EFPQ,则EF=1,M'Q=2,CE=1,∠M'EQ=60°,∴EQ=
∴PQ=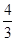 ∴射影EFPQ的面积为
∴射影EFPQ的面积为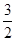 ,∵截面与平面ABC所成的二面角的大小为60°,∴截面EFN'M'的面积为
,∵截面与平面ABC所成的二面角的大小为60°,∴截面EFN'M'的面积为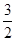 ÷cos60°=3故答案为A
÷cos60°=3故答案为A
考点:截面面积
点评:本题以直三棱柱为载体,考查截面面积的计算,搞清截面图形是解题的关键.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案设m,n是两条不同直线,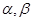 是两个不同的平面,给出下列四个命题
是两个不同的平面,给出下列四个命题
①若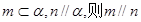 ②
②
③若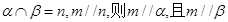 ④若
④若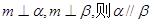
其中正确的命题是 ( )
| A.① | B.② | C.③④ | D.②④ |
已知长方体ABCD—A1B1ClD1内接于球O,底面ABCD是边长为2的正方形,E为AA1的中点,OA⊥平面BDE,则球O的表面积为
A.8 | B.16 : : | C.14 | D.18 |
如图,四面体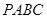 的六条边均相等,
的六条边均相等,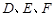 分别是
分别是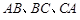 的中点,则下列四个结论中不成立的是 ( )
的中点,则下列四个结论中不成立的是 ( ) 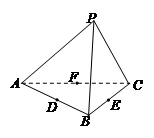
A.平面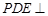 平面 平面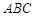 | B.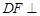 平面 平面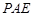 |
C. //平面 //平面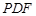 | D.平面 平面 平面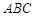 |
设 是平面
是平面 内的一条定直线,
内的一条定直线, 是平面
是平面 外的一个定点,动直线
外的一个定点,动直线 经过点
经过点 且与
且与 成
成 角,则直线
角,则直线 与平面
与平面 的交点
的交点 的轨迹是
的轨迹是
| A.圆 | B.椭圆 | C.双曲线 | D.抛物线 |
已知 是直线,
是直线, 是平面,给出下列命题:
是平面,给出下列命题:
①若 ,
, ,
, ,则
,则 或
或 .
.
②若 ,
, ,
, ,则
,则 .
.
③若m
 ,n
,n
 ,m∥
,m∥ ,n∥
,n∥ ,则
,则 ∥
∥
④若 ,
, 且
且 ,
, ,则
,则
其中正确的命题是( )。
| A.①② | B.②④ | C.②③ | D.③④ |
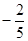
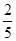
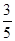
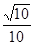
 ,过A、B分别作两平面交线的垂线,垂足为A′、B′,若
,过A、B分别作两平面交线的垂线,垂足为A′、B′,若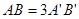 ,则AB与平面β所成的角的正弦值是( )
,则AB与平面β所成的角的正弦值是( )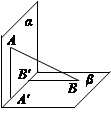
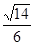
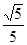
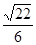
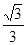
 B.
B.  C.
C. 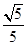 D.
D. 