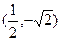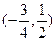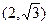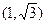题目内容
在平面直角坐标系xOy中,设P(x,y)是椭圆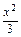 +y2=1上的一个动点,求S=x+y的最大值.
+y2=1上的一个动点,求S=x+y的最大值.
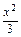 +y2=1上的一个动点,求S=x+y的最大值.
+y2=1上的一个动点,求S=x+y的最大值.当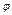 =
=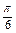 时,S取得最大值2
时,S取得最大值2
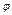 =
=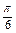 时,S取得最大值2
时,S取得最大值2由椭圆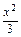 +y2=1的参数方程为
+y2=1的参数方程为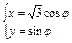 (
(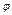 为参数),
为参数),
可设动点P的坐标为(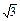 cos
cos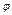 ,sin
,sin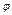 ),其中0≤
),其中0≤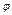 <2
<2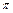 .
.
因此,S=x+y=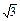 cos
cos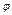 +sin
+sin
=2·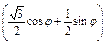 =2sin(
=2sin( +
+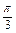 ).
).
所以当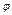 =
=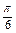 时,S取得最大值2.
时,S取得最大值2.
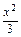 +y2=1的参数方程为
+y2=1的参数方程为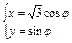 (
(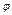 为参数),
为参数),可设动点P的坐标为(
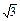 cos
cos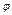 ,sin
,sin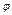 ),其中0≤
),其中0≤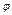 <2
<2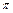 .
.因此,S=x+y=
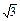 cos
cos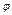 +sin
+sin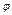
=2·
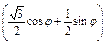 =2sin(
=2sin(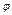 +
+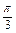 ).
).所以当
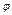 =
=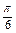 时,S取得最大值2.
时,S取得最大值2.
练习册系列答案
相关题目
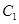
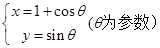 在曲线
在曲线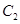
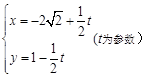 的距离最小,求出该点坐标和最小距离
的距离最小,求出该点坐标和最小距离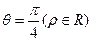 ,它与曲线C:
,它与曲线C: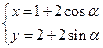 (α为参数)相交于A,B两点,则|AB|=( )
(α为参数)相交于A,B两点,则|AB|=( )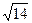
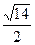
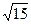
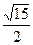





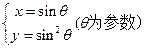 与直线
与直线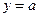 有两个公共点,则实数
有两个公共点,则实数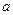 的取值范围是_________________.
的取值范围是_________________.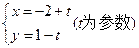 被圆
被圆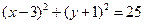 所截得的弦长为( ).
所截得的弦长为( ).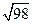
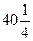

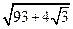
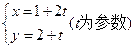 被圆
被圆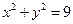 截得的弦长为( )
截得的弦长为( )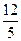
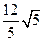
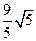
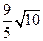
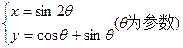 上的点是 ( )
上的点是 ( )