题目内容
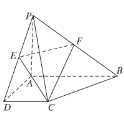
【题目】如图,四棱台![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() 底面
底面![]() ,且
,且![]() 60°,
60°,![]() ,
,![]() 是棱
是棱![]() 的中点.
的中点.
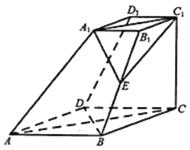
(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成线面角的正弦值.
所成线面角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由![]() 底面
底面![]() ,得
,得![]() ,再由底面
,再由底面![]() 是菱形,得
是菱形,得![]() ,利用直线与平面垂直的判定可得
,利用直线与平面垂直的判定可得![]() 平面
平面![]() ,进一步得到
,进一步得到![]() ;
;
(2)设![]() 交
交![]() 于点
于点![]() ,依题意,
,依题意,![]() 且
且![]() ,得到
,得到![]() 底面
底面![]() .以
.以![]() 为原点,
为原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系.求出平面
轴建立空间直角坐标系.求出平面![]() 的一个法向量与
的一个法向量与![]() 的坐标,再由两向量所成角的余弦值求解直线
的坐标,再由两向量所成角的余弦值求解直线![]() 与平面
与平面![]() 所成线面角的正弦值.
所成线面角的正弦值.
(1)因为![]() 底面
底面![]() ,所以
,所以![]()
因为底面![]() 是菱形,所以
是菱形,所以![]()
又![]() ,所以
,所以![]() 平面
平面![]()
又由四棱台![]() 知,
知,![]() ,
,![]() ,
,![]() ,
,![]() 四点共面
四点共面
所以![]()
(2)如图,设![]() 交
交![]() 于点
于点![]() ,依题意,
,依题意,![]() 且
且![]() ,
,
![]() ,且
,且![]() ,
,
又由已知![]() 底面
底面![]() ,得
,得![]() 底面
底面![]() .
.
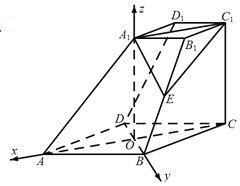
以![]() 为原点,
为原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系,如图
轴建立空间直角坐标系,如图
设![]() 交
交![]() 于点
于点![]() ,依题意,
,依题意,![]() 且
且![]() ,所以
,所以![]()
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由![]() ,得
,得![]()
因为![]() 是棱
是棱![]() 中点,所以
中点,所以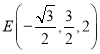
所以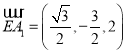 ,
,![]() ,
,![]()
设![]() 为平面
为平面![]() 的法向量
的法向量
则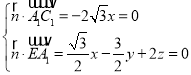 ,取
,取![]() ,得
,得![]()
设直线![]() 与平面
与平面![]() 所成线面角为
所成线面角为![]() ,则
,则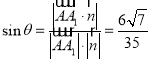
所以直线![]() 与平面
与平面![]() 所成线面角的正弦值
所成线面角的正弦值![]()

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
【题目】2020年1月底因新型冠状病毒感染的肺炎疫情形势严峻,避免外出是减少相互交叉感染最有效的方式.在家中适当锻炼,合理休息,能够提高自身免疫力,抵抗该种病毒.某小区为了调查“宅”家居民的运动情况,从该小区随机抽取了100位成年人,记录了他们某天的锻炼时间,其频率分布直方图如下:
(1)求a的值,并估计这100位居民锻炼时间的平均值![]() (同一组中的数据用该组区间的中点值代表);
(同一组中的数据用该组区间的中点值代表);
(2)小张是该小区的一位居民,他记录了自己“宅”家7天的锻炼时长:
序号n | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
锻炼时长m(单位:分钟) | 10 | 15 | 12 | 20 | 30 | 25 | 35 |
(Ⅰ)根据数据求m关于n的线性回归方程;
(Ⅱ)若![]() (
(![]() 是(1)中的平均值),则当天被称为“有效运动日”.估计小张“宅”家第8天是否是“有效运动日”?
是(1)中的平均值),则当天被称为“有效运动日”.估计小张“宅”家第8天是否是“有效运动日”?
附;在线性回归方程![]() 中,
中,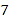 ,
,![]() .
.