题目内容
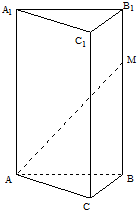如图，正三棱柱ABC-A1B1C1的底面边长为1，高为h（h＞3），点M在侧棱BB1上移动，并且M到底面ABC的距离为x，且AM与侧面BCC1B1所成的角为α．（1）若α在区间[
| π |
| 6 |
| π |
| 4 |
（2）若α为
| π |
| 6 |
分析：（1）设BC的中点为D，连接AD、DM，根据题意BB1⊥平面ABC，由线面垂直的判定与性质证出AD⊥平面BB1CC1，从而得到∠AMD即为AM与侧面BCC1所成角．然后在Rt△ADM中，设BM长为x，利用三角函数的定义建立tanα关于x的函数关系式，结合α∈[
，
]解关于x的不等式，即可得到点M到平面ABC的距离的取值范围；
（2）由（1）的结论算出BM=
．然后采用向量法：将
化成
+
，求出
•
并利用夹角公式算出
、
夹角的余弦值，最后结合异面直线所成角的范围即可求出AM与BC所成角的余弦值．
| π |
| 6 |
| π |
| 4 |
（2）由（1）的结论算出BM=
| 2 |
| AM |
| AB |
| BM |
| AM |
| BC |
| AM |
| BC |
解答：解：（1）设BC的中点为D，连接AD、DM，则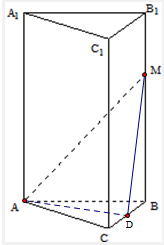
∵△ABC为正三角形，D为AC中点，∴AD⊥BC，
∵BB1⊥平面ABC，AD?平面ABC，∴AD⊥BB1
∵BB1、BC是平面BB1C1C内的相交直线，∴AD⊥平面BB1CC1．
因此，∠AMD即为AM与侧面BCC1所成角α．
∵点M到平面ABC的距离为BM，设BM=x，x∈（0，h）．
在Rt△ADM中，tan∠AMD=
．
由AD=
，DM=
=
，得tanα=
．
∵α∈[
，
]时，tanα∈[
，1]
∴
≤
≤1，化简得3≤1+4x2≤9，解得
≤x2≤2．
因此，点M到平面ABC的距离x的取值范围是[
，
]；
（2）当α=
时，由（1）得BM=
，
故可得DM=
，AM=
=
．
设
与
的夹角为θ．
∵
•
=（
+
）•
=
•
+
•
=1×1×cos120°+0=-
．
∴cos＜
，
＞=
=
=-
∵AM与BC所成角θ∈(0，
]，
∴cosθ=
，即AM与BC所成角的余弦值
．
∵△ABC为正三角形，D为AC中点，∴AD⊥BC，
∵BB1⊥平面ABC，AD?平面ABC，∴AD⊥BB1
∵BB1、BC是平面BB1C1C内的相交直线，∴AD⊥平面BB1CC1．
因此，∠AMD即为AM与侧面BCC1所成角α．
∵点M到平面ABC的距离为BM，设BM=x，x∈（0，h）．
在Rt△ADM中，tan∠AMD=
| AD |
| DM |
由AD=
| ||
| 2 |
| BD2+BM2 |
| ||
| 2 |
| ||
|
∵α∈[
| π |
| 6 |
| π |
| 4 |
| ||
| 3 |
∴
| ||
| 3 |
| ||
|
| 1 |
| 2 |
因此，点M到平面ABC的距离x的取值范围是[
| ||
| 2 |
| 2 |
（2）当α=
| π |
| 6 |
| 2 |
故可得DM=
| 3 |
| 2 |
| AD2+DM2 |
| 3 |
设
| AM |
| BC |
∵
| AM |
| BC |
| AB |
| BM |
| BC |
| AB |
| BC |
| BM |
| BC |
| 1 |
| 2 |
∴cos＜
| AM |
| BC |
| ||||
|
-
| ||
|
| ||
| 6 |
∵AM与BC所成角θ∈(0，
| π |
| 2 |
∴cosθ=
| ||
| 6 |
| ||
| 6 |
点评：本题在特殊三棱柱中求异面直线所成的角，着重考查了直棱柱的性质、线面垂直的判定定理和异面直线所成角的定义及其求法等知识，属于中档题．
练习册系列答案
相关题目
如图，正三棱柱ABC-A1B1C1各棱长都等于a，E是BB1的中点．
如图，正三棱柱ABC-A1B1C1的各棱长都2，E，F分别是AB，A1C1的中点，则EF的长是（ ）| A、2 | ||
B、
| ||
C、
| ||
D、
|
如图，正三棱柱ABC-A1B1C1的所有棱长都为2，D为CC1中点．
（2013•郑州二模）如图，正三棱柱ABC-A1B1C1的所有棱长都为2，D为CC1中点．
如图，正三棱柱ABC-A1B1C1中（注：底面为正三角形且侧棱与底面垂直），BC=CC1=2，P，Q分别为BB1，CC1的中点．