题目内容
函数 的定义域为
的定义域为 ,若
,若 且
且 时总有
时总有 ,则称
,则称 为单函数.例如,函数
为单函数.例如,函数 是单函数.下列命题:
是单函数.下列命题:
①函数 是单函数;
是单函数;
②函数 是单函数;
是单函数;
③若 为单函数,
为单函数, 且
且 ,则
,则 ;
;
④函数 在定义域内某个区间
在定义域内某个区间 上具有单调性,则
上具有单调性,则 一定是单函数.
一定是单函数.
其中的真命题是_________.(写出所有真命题的编号)
③
解析试题分析:根据单函数的定义可知如果函数 为单函数,则函数
为单函数,则函数 在其定义域上一定是单调递增或单调递减函数,即该函数为一一对应关系,据此分析可知①不是,因为该二次函数先减后增;②不是,因为该函数是先减后增;显然④的说话也不对,故真命题是③.
在其定义域上一定是单调递增或单调递减函数,即该函数为一一对应关系,据此分析可知①不是,因为该二次函数先减后增;②不是,因为该函数是先减后增;显然④的说话也不对,故真命题是③.
考点:新定义、函数的单调性,考查学生的分析、理解能力.

练习册系列答案
相关题目
 ,满足
,满足 ,且
,且 ,若在区间
,若在区间 上,不等式
上,不等式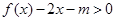 恒成立,则实数m的取值范围为 .
恒成立,则实数m的取值范围为 . 上的函数
上的函数 ,满足
,满足 ,
, ,则
,则 .
. ,则
,则 (用含
(用含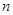 的式子表示).
的式子表示). 的单调递减区间是 .
的单调递减区间是 . ,其中
,其中 、
、 为常数,且
为常数,且 ,若
,若 为常数,则
为常数,则 的值为 .
的值为 . 在区间
在区间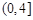 上是增函数,则实数
上是增函数,则实数 的取值范围为 .
的取值范围为 . 的解所在区间为
的解所在区间为 ,则
,则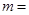 .
. 有三个不同的零点,则实数
有三个不同的零点,则实数 的取值范围是_____.
的取值范围是_____.
 ,则
,则 所对应的
所对应的 的零点的取值集合为 .
的零点的取值集合为 . ______.(写出所有正确结论的序号)
______.(写出所有正确结论的序号)

