题目内容
8.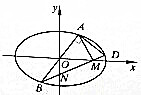 对于椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),c为椭圆半焦距,e为椭圆离心率,过原点O的直线与椭圆C交于A、B两点(A、B不是椭圆C的顶点),点D在椭圆C上,且AD⊥AB,直线BD与x轴、y轴分别交于M、N两点,证明:
对于椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),c为椭圆半焦距,e为椭圆离心率,过原点O的直线与椭圆C交于A、B两点(A、B不是椭圆C的顶点),点D在椭圆C上,且AD⊥AB,直线BD与x轴、y轴分别交于M、N两点,证明:(1)当e≠$\frac{\sqrt{2}}{2}$时,设直线BD、AM的斜率分别为k1、k2,则k1=(1-2e2)k2,当e=$\frac{\sqrt{2}}{2}$时,则直线AM与x轴垂直;
(2)△OMN面积的最大值为$\frac{{c}^{4}}{4ab}$.
分析 (1)设出A,D的坐标分别为(x1,y1)(x1y1≠0),(x2,y2),用A的坐标表示B的坐标,把AB和AD的斜率都用A的坐标表示,写出直线AD的方程,和椭圆方程联立后利用根与系数关系得到AD横纵坐标的和,求出AD中点坐标,则BD斜率可求,再写出BD所在直线方程,取y=0得到M点坐标,由两点求斜率得到AM的斜率,讨论离心率e,即可得证;
(2)由BD方程求出N点坐标,结合(1)中求得的M的坐标得到△OMN的面积,然后结合椭圆方程利用椭圆的参数方程,结合二倍角公式和正弦函数的值域,可求得最值.
解答 证明:(1)设A(x1,y1)(x1y1≠0),D(x2,y2),
则B(-x1,-y1).
∵直线AB的斜率kAB=$\frac{{y}_{1}}{{x}_{1}}$,
又AB⊥AD,
∴直线AD的斜率kAD=-$\frac{{x}_{1}}{{y}_{1}}$.
设AD方程为y=kx+m,
由题意知k≠0,m≠0.
联立椭圆方程$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,得
(b2+a2k2)x2+2ka2mx+a2m2-a2b2=0.
∴x1+x2=-$\frac{2k{a}^{2}m}{{b}^{2}+{a}^{2}{k}^{2}}$.
因此y1+y2=k(x1+x2)+2m=$\frac{2m{b}^{2}}{{b}^{2}+{a}^{2}{k}^{2}}$.
由题意可得k1=$\frac{{y}_{1}+{y}_{2}}{{x}_{1}+{x}_{2}}$=-$\frac{{b}^{2}}{k{a}^{2}}$=$\frac{{{b}^{2}y}_{1}}{{{a}^{2}x}_{1}}$.
∴直线BD的方程为y+y1=$\frac{{{b}^{2}y}_{1}}{{{a}^{2}x}_{1}}$(x+x1).
令y=0,得x=$\frac{{a}^{2}-{b}^{2}}{{b}^{2}}$x1,即M($\frac{{a}^{2}-{b}^{2}}{{b}^{2}}$x1,0).
可得k2=-$\frac{{y}_{1}}{{x}_{1}-\frac{{a}^{2}-{b}^{2}}{{b}^{2}}{x}_{1}}$.
∴当e≠$\frac{\sqrt{2}}{2}$时,即a2-b2≠b2,
k1=$\frac{2{b}^{2}-{a}^{2}}{{a}^{2}}$k2=$\frac{{a}^{2}-2{c}^{2}}{{a}^{2}}$k2=(1-2e2)k2;
当e=$\frac{\sqrt{2}}{2}$时,a2-b2=b2,即有M(x1,0),
即直线AM与x轴垂直;
(2)直线BD的方程为y+y1=$\frac{{{b}^{2}y}_{1}}{{{a}^{2}x}_{1}}$(x+x1).
令x=0,得y=$\frac{{b}^{2}-{a}^{2}}{{a}^{2}}$y1,即N(0,$\frac{{b}^{2}-{a}^{2}}{{a}^{2}}$y1),
由(1)知M($\frac{{a}^{2}-{b}^{2}}{{b}^{2}}$x1,0).
可得△OMN的面积为S=$\frac{1}{2}$•$\frac{{a}^{2}-{b}^{2}}{{b}^{2}}$|x1|•$\frac{{a}^{2}-{b}^{2}}{{a}^{2}}$|y1|=$\frac{({a}^{2}-{b}^{2})^{2}}{2{a}^{2}{b}^{2}}$|acosα•bsinα|
=$\frac{1}{4}$$\frac{({a}^{2}-{b}^{2})^{2}}{ab}$•|sin2α|≤$\frac{{c}^{4}}{4ab}$,
当且仅当α=$\frac{kπ}{2}$±$\frac{π}{4}$,k∈Z.
∴△OMN面积的最大值为$\frac{{c}^{4}}{4ab}$.
点评 本题主要考查了直线与椭圆的位置关系的应用,直线与曲线联立,根据方程的根与系数的关系解题,是处理这类问题的最为常用的方法,但圆锥曲线的特点是计算量比较大,要求考试具备较强的运算推理的能力,是难题.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案| A. | 99 | B. | 100 | C. | 101 | D. | 102 |
| A. | 反证法是逆推法 | B. | 合情推理得到的结论都是正确的 | ||
| C. | 演绎推理可以作为证明的步骤 | D. | 分析法是间接证法 |
| A. | $\sqrt{14}$ | B. | $3\sqrt{2}$ | C. | $2\sqrt{5}$ | D. | $\sqrt{26}$ |