题目内容
18.长方体ABCD-A′B′C′D′中,长、宽、高分别为3,2,1,一只蚂蚁从点A出发沿着长方体的表面爬行到达点C'的最短路程是( )| A. | $\sqrt{14}$ | B. | $3\sqrt{2}$ | C. | $2\sqrt{5}$ | D. | $\sqrt{26}$ |
分析 将长方形的盒子按不同方式展开,得到不同的矩形,求出不同矩形的对角线,最短者即为正确答案.
解答 解:将长方形的盒子按不同方式展开,得到不同的矩形,对角线长分别为:
$\sqrt{{3}^{2}+(2+1)^{2}}$=3$\sqrt{2}$;$\sqrt{{2}^{2}+(3+1)^{2}}$=2$\sqrt{5}$,$\sqrt{{1}^{2}+(3+2)^{2}}$=$\sqrt{26}$,
∴从点A出发沿着长方体的表面爬行到达点C'的最短路程是3$\sqrt{2}$.
故选:B.
点评 此题考查了两点之间线段最短,解答时要进行分类讨论,利用勾股定理是解题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
13.从某初中随机选取5名男生,其身高和体重的数据表如表,其回归直线方程为$\hat y=0.56x-26.2$,由于受到污损,使得一个数据辨别不清,求污损数据为66.
| 身高x(cm) | 160 | 165 | 170 | 175 | 180 |
| 体重y(kg) | 63 | 70 | 72 | 74 |
10.在2015年春节期间,某市物价部门,对本市五个商场销售的某商品一天的销售量及其价格进行调查,五个商场的售价x元和销售量y件之间的一组数据如表所示:
通过分析,发现销售量y对商品的价格x具有线性相关关系,且$\widehat{b}$=-3.2,则销售量y对商品的价格x的回归直线方程为$\widehat{y}$=-3.2x+40.
| 价格x | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y | 11 | 10 | 8 | 6 | 5 |
7.已知二次函数y=x2-2ax+1在区间(2,3)上是单调函数,则实数a的取值范围是( )
| A. | a≤-3或a≥-2 | B. | 2≤a≤3 | C. | a≤2或a≥3 | D. | -3≤a≤-2 |
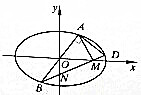 对于椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),c为椭圆半焦距,e为椭圆离心率,过原点O的直线与椭圆C交于A、B两点(A、B不是椭圆C的顶点),点D在椭圆C上,且AD⊥AB,直线BD与x轴、y轴分别交于M、N两点,证明:
对于椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),c为椭圆半焦距,e为椭圆离心率,过原点O的直线与椭圆C交于A、B两点(A、B不是椭圆C的顶点),点D在椭圆C上,且AD⊥AB,直线BD与x轴、y轴分别交于M、N两点,证明: