题目内容
【题目】已知函数![]() R.
R.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 有两个零点,求实数
有两个零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1) 当a≤0,![]() 在(0,2)上单调递增,在(2,+∞)递减;当
在(0,2)上单调递增,在(2,+∞)递减;当![]() ,
,![]() 在(0,2)和
在(0,2)和![]() 上单调递增,在(2,
上单调递增,在(2,![]() )递减;当a=
)递减;当a=![]() ,
,![]() 在(0,+∞)递增;当a>
在(0,+∞)递增;当a>![]() ,
,![]() 在(0,
在(0,![]() )和(2,+∞)上单调递增,在(
)和(2,+∞)上单调递增,在(![]() ,2)递减;(2)
,2)递减;(2) ![]() .
.
【解析】
(1)求出![]() ,分四种情况讨论
,分四种情况讨论![]() 的范围,在定义域内,分别令
的范围,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间,![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(2)由(1)知当
的减区间;(2)由(1)知当![]() 时,
时,![]() 单调递增区间为
单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,又
,又![]() ,取
,取![]() ,可证明
,可证明![]() ,
,![]() 有两个零点等价于
有两个零点等价于![]() ,得
,得![]() ,可证明,当
,可证明,当![]() 时与当
时与当![]() 且
且![]() 时,至多一个零点,综合讨论结果可得结论.
时,至多一个零点,综合讨论结果可得结论.
(1)![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
(i)当![]() 时,
时,![]() 恒成立,
恒成立,
![]() 时,
时,![]() 在
在![]() 上单调递增;
上单调递增;
![]() 时,
时,![]() 在
在![]() 上单调递减.
上单调递减.
(ii)当![]() 时,由
时,由![]() 得,
得,![]() (舍去),
(舍去),
①当![]() ,即
,即![]() 时,
时,![]() 恒成立,
恒成立,![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() ,即
,即![]() 时,
时,![]() 或
或![]() ,
,
![]() 恒成立,
恒成立,![]() 在
在![]() 上单调递增;
上单调递增;
![]() 时,
时,![]() 恒成立,
恒成立,![]() 在
在![]() 上单调递减.
上单调递减.
③当![]() ,即
,即![]() 时,
时,![]() 或
或![]() 时,
时,![]() 恒成立,
恒成立,
![]() 在
在![]() 单调递增,
单调递增,
![]() 时,
时,![]() 恒成立,
恒成立,![]() 在
在![]() 上单调递减.
上单调递减.
综上,当![]() 时,
时,![]() 单调递增区间为
单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
当![]() 时,
时,![]() 单调递增区间为
单调递增区间为![]() ,无单调递减区间为;
,无单调递减区间为;
当![]() 时,
时,![]() 单调递增区间为
单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)由(1)知当![]() 时,
时,![]() 单调递增区间为
单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,
,
又![]() ,取
,取![]() ,令
,令![]() ,
,
则![]() 在
在![]() 成立,故
成立,故![]() 单调递增,
单调递增,
![]() ,
,
![]() ,
,
![]() 有两个零点等价于
有两个零点等价于![]() ,得
,得![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,只有一个零点,不符合题意;
,只有一个零点,不符合题意;
当![]() 时,
时,![]() 在
在![]() 单调递增,至多只有一个零点,不符合题意;
单调递增,至多只有一个零点,不符合题意;
当![]() 且
且![]() 时,
时,![]() 有两个极值,
有两个极值,
![]() ,
,
记![]() ,
,
![]() ,
,
令![]() ,则
,则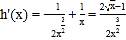 ,
,
当![]() 时,
时,![]() 在
在![]() 单调递增;
单调递增;
当![]() 时,
时,![]() 在
在![]() 单调递减,
单调递减,
故![]() 在
在![]() 单调递增,
单调递增,
![]() 时,
时,![]() ,故
,故![]() ,
,
又![]() ,
,
由(1)知,![]() 至多只有一个零点,不符合题意,
至多只有一个零点,不符合题意,
综上,实数![]() 的取值范围为
的取值范围为![]() .
.

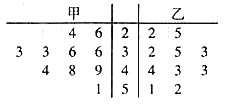
【题目】大型综艺节目《最强大脑》中,有一个游戏叫做盲拧魔方,就是玩家先观察魔方状态并进行记忆,记住后蒙住眼睛快速还原魔方,盲拧在外人看来很神奇,其实原理是十分简单的,要学会盲拧也是很容易的.为了解某市盲拧魔方爱好者的水平状况,某兴趣小组在全市范围内随机抽取了![]() 名魔方爱好者进行调查,得到的情况如表所示:
名魔方爱好者进行调查,得到的情况如表所示:
用时(秒) |
|
|
|
|
男性人数 | 15 | 22 | 14 | 9 |
女性人数 | 5 | 11 | 17 | 7 |
附: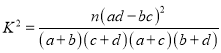 ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
(1)将用时低于![]() 秒的称为“熟练盲拧者”,不低于
秒的称为“熟练盲拧者”,不低于![]() 秒的称为“非熟练盲拧者”.请根据调查数据完成以下
秒的称为“非熟练盲拧者”.请根据调查数据完成以下![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为是否为“熟练盲拧者”与性别有关?
的把握认为是否为“熟练盲拧者”与性别有关?
熟练盲拧者 | 非熟练盲拧者 | |
男性 | ||
女性 |
(2)以这![]() 名盲拧魔方爱好者的用时不超过
名盲拧魔方爱好者的用时不超过![]() 秒的频率,代替全市所有盲拧魔方爱好者的用时不超过
秒的频率,代替全市所有盲拧魔方爱好者的用时不超过![]() 秒的概率,每位盲拧魔方爱好者用时是否超过
秒的概率,每位盲拧魔方爱好者用时是否超过![]() 秒相互独立.那么在该兴趣小组在全市范围内再次随机抽取
秒相互独立.那么在该兴趣小组在全市范围内再次随机抽取![]() 名爱好者进行测试,其中用时不超过
名爱好者进行测试,其中用时不超过![]() 秒的人数最有可能(即概率最大)是多少?
秒的人数最有可能(即概率最大)是多少?
【题目】某知名电商在![]() 双十一购物狂欢节中成交额再创新高,
双十一购物狂欢节中成交额再创新高,![]() 月
月![]() 日单日成交额达
日单日成交额达![]() 亿元.某店主在此次购物狂欢节期间开展了促销活动,为了解买家对此次促销活动的满意情况,随机抽取了参与活动的
亿元.某店主在此次购物狂欢节期间开展了促销活动,为了解买家对此次促销活动的满意情况,随机抽取了参与活动的![]() 位买家,调查了他们的年龄层次和购物满意情况,得到年龄层次的频率分布直方图和“购物评价为满意”的年龄层次频数分布表.年龄层次的频率分布直方图:
位买家,调查了他们的年龄层次和购物满意情况,得到年龄层次的频率分布直方图和“购物评价为满意”的年龄层次频数分布表.年龄层次的频率分布直方图:
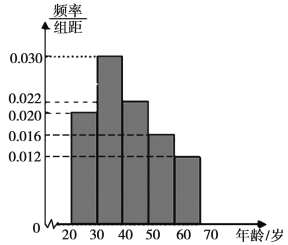
“购物评价为满意”的年龄层次频数分布表:
年龄(岁) |
|
|
|
|
|
频数 |
|
|
|
|
|
(1)估计参与此次活动的买家的平均年龄(同一组中的数据用该组区间的中点值做代表);
(2)若年龄在![]() 岁以下的称为“青年买家”,年龄在
岁以下的称为“青年买家”,年龄在![]() 岁以上(含
岁以上(含![]() 岁)的称为“中年买家”,完成下面的列联表,并判断能否有
岁)的称为“中年买家”,完成下面的列联表,并判断能否有![]() 的把握认为中、青年买家对此次活动的评价有差异?
的把握认为中、青年买家对此次活动的评价有差异?
评价满意 | 评价不满意 | 合计 | |
中年买家 | |||
青年买家 | |||
合计 |
|
附:参考公式: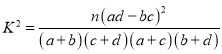 .
.
|
|
|
|
|
|
|
|
【题目】随着食品安全问题逐渐引起人们的重视,有机、健康的高端绿色蔬菜越来越受到消费者的欢迎,同时生产—运输—销售一体化的直销供应模式,不仅减少了成本,而且减去了蔬菜的二次污染等问题.
(1)在有机蔬菜的种植过程中,有机肥料使用是必不可少的.根据统计某种有机蔬菜的产量与有机肥料的用量有关系,每个有机蔬菜大棚产量的增加量![]() (百斤)与使用堆沤肥料
(百斤)与使用堆沤肥料![]() (千克)之间对应数据如下表
(千克)之间对应数据如下表
使用堆沤肥料 | 2 | 4 | 5 | 6 | 8 |
产量的增加量 | 3 | 4 | 4 | 4 | 5 |
依据表中的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;并根据所求线性回归方程,估计如果每个有机蔬菜大棚使用堆沤肥料10千克,则每个有机蔬菜大棚产量增加量
;并根据所求线性回归方程,估计如果每个有机蔬菜大棚使用堆沤肥料10千克,则每个有机蔬菜大棚产量增加量![]() 是多少百斤?
是多少百斤?
(2)某大棚蔬菜种植基地将采摘的有机蔬菜以每份三斤称重并保鲜分装,以每份10元的价格销售到生鲜超市.“乐购”生鲜超市以每份15元的价格卖给顾客,如果当天前8小时卖不完,则超市通过促销以每份5元的价格卖给顾客(根据经验,当天能够把剩余的有机蔬菜都低价处理完毕,且处理完毕后,当天不再进货).该生鲜超市统计了100天有机蔬菜在每天的前8小时内的销售量(单位:份),制成如下表格(注:![]() ,且
,且![]() );
);
前8小时内的销售量(单位:份) | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
频数 | 10 | x | 16 | 6 | 15 | 13 | y |
若以100天记录的频率作为每日前8小时销售量发生的概率,该生鲜超市当天销售有机蔬菜利润的期望值为决策依据,当购进17份比购进18份的利润的期望值大时,求![]() 的取值范围.
的取值范围.
附:回归直线方程为![]() ,其中
,其中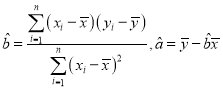 .
.