题目内容
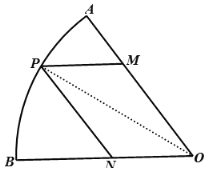
【题目】某居民小区为缓解业主停车难的问题,拟对小区内一块扇形空地![]() 进行改建.如图所示,平行四边形
进行改建.如图所示,平行四边形![]() 区域为停车场,其余部分建成绿地,点
区域为停车场,其余部分建成绿地,点![]() 在围墙
在围墙![]() 弧上,点
弧上,点![]() 和点
和点![]() 分别在道路
分别在道路![]() 和道路
和道路![]() 上,且
上,且![]() 米,
米,![]() ,设
,设![]() .
.
(1)求停车场面积![]() 关于
关于![]() 的函数关系式,并指出
的函数关系式,并指出![]() 的取值范围;
的取值范围;
(2)当![]() 为何值时,停车场面积
为何值时,停车场面积![]() 最大,并求出最大值(精确到
最大,并求出最大值(精确到![]() 平方米).
平方米).
【答案】(1)![]() ,
, ![]()
(2)当![]() 时,停车场最大面积为
时,停车场最大面积为![]() 平方米
平方米
【解析】
(1)由正弦定理求得![]() ,再计算停车场面积
,再计算停车场面积![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)化简函数解析式![]() ,求出
,求出![]() 的最大值以及取最大值时对应
的最大值以及取最大值时对应![]() 的值.
的值.
解:(1)由平行四边形![]() 得,在
得,在![]() 中,
中,![]() ,
,![]() ,
,
则![]() ,即
,即![]() ,
,
即![]() ,
,![]() ,
,
则停车场面积![]() ,
,
即![]() ,其中
,其中![]() .
.
(2)由(1)得![]() ,
,
即![]() ,
,
则![]() .
.
因为![]() ,所以
,所以![]() ,
,
则![]() 时,
时,![]() 平方米.
平方米.
故当![]() 时,停车场最大面积为
时,停车场最大面积为![]() 平方米.
平方米.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
【题目】某品牌奶茶公司计划在A地开设若干个连锁加盟店,经调查研究,加盟店的个数x与平均每个店的月营业额y(万元)具有如下表所示的数据关系:
x | 2 | 4 | 6 | 8 | 10 |
y | 20.9 | 20.2 | 19 | 17.8 | 17.1 |
(1)求y关于x的线性回归方程;
(2)根据(1)中的结果分析,为了保证平均每个加盟店的月营业额不少于14.6万元,则A地开设加盟店的个数不能超过几个?
参考公式:线性回归方程![]() 中的斜率和截距的最小二乘估计公式分别为
中的斜率和截距的最小二乘估计公式分别为
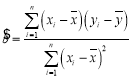 ,
,![]()