题目内容
【题目】社区服务是综合实践活动课程的重要内容，某市教育部门在全市高中学生中随机抽取200位学生参加社区服务的数据，按时间段
，
，
，
，
（单位：小时）进行统计，其频率分布直方图如图所示.
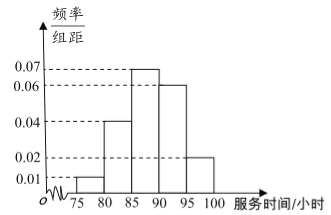
（1）求抽取的200位学生中，参加社区服务时间不少于90小时的学生人数，并估计从全市高中学生中任意选取一人，其参加社区服务时间不少于90小时的概率；
（2）从全市高中学生（人数很多）中任意选取3位学生，记
为3位学生中参加社区服务时间不少于90小时的人数，试求随机变量
的分布列和数学期望
.
【答案】（1）
；（2）分布列见解析，
【解析】
试题分析：（1）由频率分布直方图可求出抽取的
位学生中，参加社区服务时间不少于
小时的学生人数为
人，再根据古典概型概率公式可得结果；（2）随机变量
的可能取值为
分别求出对应的概率，再利用期望公式求解.
试题解析：（1）根据题意，
参加社区服务在时间段
的学生人数为
人；
参加社区服务在时间段
的学生人数为
人；
∴抽取的200位学生中，参加社区服务时间不少于90小时的学生人数为80人.
∴从全市高中学生中任意选取一人，其参加社区服务时间不少于90小时的概率为
.
（2）由（1）可知，从全市高中学生中任意选取1人，其参加社区服务时间不少于90小时的概率为
.
由已知得，随机变量的可能取值为0,1,2,3，
则
，
，
，
，
随机变量
的分布列为
∴
.
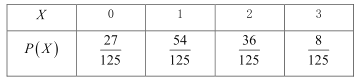
练习册系列答案
阅读快车系列答案
相关题目
