题目内容
如图所示,四棱锥P-ABCD中,PD⊥平面ABCD,PA与平面ABCD所成的角为60°,在四边形ABCD中,∠D=∠DAB=90°,AB=4,CD=1,AD=2.(1)建立适当的坐标系,并写出点B,P的坐标;
(2)求异面直线PA与BC所成角的余弦值.

【答案】分析:(1)以D为原点,射线DA,DC,DP分别为x,y,z轴的正方向,建立空间直角坐标系D-xyz,求出点B,P的坐标即可;
(2)先求异面直线PA与BC所在向量的坐标,再根据向量的夹角公式求出所成角.
解答: 解:(1)如图所示,以D为原点,射线DA,DC,DP分别为x,y,z轴的正方向,
解:(1)如图所示,以D为原点,射线DA,DC,DP分别为x,y,z轴的正方向,
建立空间直角坐标系D-xyz.
∵∠D=∠DAB=90°,AB=4,CD=1,AD=2,
∴A(2,0,0),C(0,1,0),B(2,4,0),
由PD⊥平面ABCD,得∠PAD为PA与平面ABCD所成的角,
∴∠PAD=60°.
在Rt△PAD中,由AD=2,得PD=2 ,
,
∴P(0,0,2 ).
).
(2)∵=(2,0,-2 ),
),
=(-2,-3,0),
∴cos<PA,BC>= =-
=- ,
,
所以PA与BC所成角的余弦值为
点评:本小题主要考查异面直线所成的角、平面与平面垂直、坐标运算等基础知识,考查空间想象能力,运算能力和推理论证能力.
(2)先求异面直线PA与BC所在向量的坐标,再根据向量的夹角公式求出所成角.
解答:
 解:(1)如图所示,以D为原点,射线DA,DC,DP分别为x,y,z轴的正方向,
解:(1)如图所示,以D为原点,射线DA,DC,DP分别为x,y,z轴的正方向,建立空间直角坐标系D-xyz.
∵∠D=∠DAB=90°,AB=4,CD=1,AD=2,
∴A(2,0,0),C(0,1,0),B(2,4,0),
由PD⊥平面ABCD,得∠PAD为PA与平面ABCD所成的角,
∴∠PAD=60°.
在Rt△PAD中,由AD=2,得PD=2
 ,
,∴P(0,0,2
 ).
).(2)∵=(2,0,-2
 ),
),=(-2,-3,0),
∴cos<PA,BC>=
 =-
=- ,
,所以PA与BC所成角的余弦值为

点评:本小题主要考查异面直线所成的角、平面与平面垂直、坐标运算等基础知识,考查空间想象能力,运算能力和推理论证能力.

练习册系列答案
相关题目
 如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.
如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.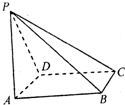 如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4,
如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4,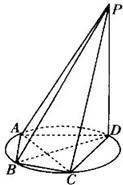 如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD.
如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD. (2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点.
(2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点. 如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.
如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.