题目内容
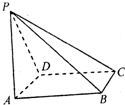 如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4,
如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4,∠PAD=60°.求:
(1)四棱锥P-ABCD的体积.
(2)二面角P-BC-D的正切值.
分析:(1)由已知中四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4,∠PAD=60°,我们在平面PAD中作PE⊥AD,交AD的延长线与E,则PE即为棱锥底面上的高,求出棱锥的底面面积及高,代入棱锥体积公式即可得到答案.
(2)作EF∥DC,交BC的延长线与F,连接PF,于是∠PEF是二面角P-BC-D的平面角,解三角形PEF,即可得到二面角P-BC-D的正切值.
(2)作EF∥DC,交BC的延长线与F,连接PF,于是∠PEF是二面角P-BC-D的平面角,解三角形PEF,即可得到二面角P-BC-D的正切值.
解答: 解:(1)∵AB⊥AD、AB⊥AP,
解:(1)∵AB⊥AD、AB⊥AP,
∴AB⊥平面PAD.
由AB?平面ABCD,
∴平面ABCD⊥平面PAD,
在平面PAD中,作作PE⊥AD,交AD的延长线与E.(因为AE=APcos60°=2>AD)
∴平面ABCD⊥PE,在Rt△PAE中,PE=APsin60°=2
VP-ABCD=
AB•AD•PE=2
(6分)
(2)在平面ABCD中,作EF∥DC,交BC的延长线与F,则EF⊥BF,连接PF.∵PE⊥平面ABCD,EF⊥BF∴PF⊥BF
于是∠PEF是二面角P-BC-D的平面角. (10分)
在Rt△PEF中,tan∠PEF=
=
(12分)
 解:(1)∵AB⊥AD、AB⊥AP,
解:(1)∵AB⊥AD、AB⊥AP,∴AB⊥平面PAD.
由AB?平面ABCD,
∴平面ABCD⊥平面PAD,
在平面PAD中,作作PE⊥AD,交AD的延长线与E.(因为AE=APcos60°=2>AD)
∴平面ABCD⊥PE,在Rt△PAE中,PE=APsin60°=2
| 3 |
VP-ABCD=
| 1 |
| 3 |
| 3 |
(2)在平面ABCD中,作EF∥DC,交BC的延长线与F,则EF⊥BF,连接PF.∵PE⊥平面ABCD,EF⊥BF∴PF⊥BF
于是∠PEF是二面角P-BC-D的平面角. (10分)
在Rt△PEF中,tan∠PEF=
| PF |
| EF |
2
| ||
| 3 |
点评:本题考查的知识点是二面角的平面角及其求法,棱锥的体积,其中(1)的关键是计算出棱锥底面上的高,(2)的关键是确定二面角P-BC-D的平面角.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.
如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.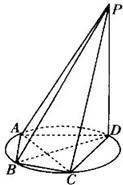 如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD.
如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD. (2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点.
(2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点. 如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.
如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.