题目内容
（2012•烟台一模）如图所示，四棱锥P-ABCD中，ABCD为正方形，PA⊥AD，E，F，G分别是线段PA，PD，CD的中点．求证：
（1）BC∥平面EFG；
（2）平面EFG⊥平面PAB．
分析：（1）欲证BC∥平面EFG，根据直线与平面平行的判定定理可知只需证BC与平面EFG内直线平行，而EF∥BC，BC?平面EFG，EF?平面EFG，满足定理条件；
（2）欲证平面EFG⊥平面PAB，只需证明EF⊥平面PAB即可，PA⊥EF，AB⊥EF，PA∩AB=A即可证明．
（2）欲证平面EFG⊥平面PAB，只需证明EF⊥平面PAB即可，PA⊥EF，AB⊥EF，PA∩AB=A即可证明．
解答：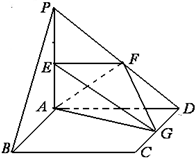
（1）证明：∵E，F分别是线段PA、PD的中点，∴EF∥AD．…（2分）
又∵ABCD为正方形，∴BC∥AD，∴EF∥BC．…（4分）
又∵BC?平面EFG，EF?平面EFG，
∴BC∥平面EFG．…（6分）
（2）证明：∵PA⊥AD，又EF∥AD，
∴PA⊥EF．…（8分）
又ABCD为正方形，∴AB⊥EF，
又PA∩AB=A，∴EF⊥平面PAB，…（10分）
又EF?平面EFG，
∴平面EFG⊥平面PAB．…（12分）
（1）证明：∵E，F分别是线段PA、PD的中点，∴EF∥AD．…（2分）又∵ABCD为正方形，∴BC∥AD，∴EF∥BC．…（4分）
又∵BC?平面EFG，EF?平面EFG，
∴BC∥平面EFG．…（6分）
（2）证明：∵PA⊥AD，又EF∥AD，
∴PA⊥EF．…（8分）
又ABCD为正方形，∴AB⊥EF，
又PA∩AB=A，∴EF⊥平面PAB，…（10分）
又EF?平面EFG，
∴平面EFG⊥平面PAB．…（12分）
点评：本题主要考查了直线与平面垂直的判定，以及直线与平面所成的角，考查空间想象能力、运算能力和推理论证能力，属于基础题．
练习册系列答案
相关题目