题目内容
设二次函数f(x)=mx2+nx+t的图像过原点,g(x)=ax3+bx?3(x>0),f(x), g(x)的导函数为 ,g¢(x),且
,g¢(x),且 ="0,"
="0,"  =?2,f(1)="g(1),"
=?2,f(1)="g(1),"  =g¢(1).
=g¢(1).
(Ⅰ)求函数f(x),g(x)的解析式;
(Ⅱ)求F(x)=f(x)?g(x)的极小值;
(Ⅲ)是否存在实常数k和m,使得f(x)³kx+m和g(x)£kx+m成立?若存在,求出k和m的值;若不存在,说明理由.
 ,g¢(x),且
,g¢(x),且 ="0,"
="0,"  =?2,f(1)="g(1),"
=?2,f(1)="g(1),"  =g¢(1).
=g¢(1).(Ⅰ)求函数f(x),g(x)的解析式;
(Ⅱ)求F(x)=f(x)?g(x)的极小值;
(Ⅲ)是否存在实常数k和m,使得f(x)³kx+m和g(x)£kx+m成立?若存在,求出k和m的值;若不存在,说明理由.
(Ⅰ)由已知得t=0,
 =2mx+n,
=2mx+n,则
 ="n=0,"
="n=0,"  =?2m+n=?2,从而n="0," m=1,
=?2m+n=?2,从而n="0," m=1,∴f(x)=x2.
则
 ="2x, " g¢(x)=3ax2+b.
="2x, " g¢(x)=3ax2+b.由f(1)="g(1),"
 =g¢(1)得a+b?3=2,3a+b=2,解得a=?1,b=5,
=g¢(1)得a+b?3=2,3a+b=2,解得a=?1,b=5,∴g(x)=?x3+5x?3(x>0) ……4分
(Ⅱ)∵F(x)=f(x)?g(x)=x3+x2?5x+3(x>0),
求导数得F¢(x)=3x2+2x?5=(x?1)(3x+5)
∴F(x)在(0,1)单调递减,在(1,+¥)单调递增,从而F(x)的极小值为F(1)="0. " ……8分
(Ⅲ)因 f(x)与g(x)有一个公共点(1,1),而函数f(x)在点(1,1)的切线方程为y=2x?1.
下面验证
 都成立即可.
都成立即可.由(x?1)2=x2?2x+1³0,得x2³2x?1,知f(x)³2x?1恒成立.
设h(x)=?x3+5x?3?(2x?1)= ?x3+3x?2(x)>0,
求导数得h¢(x)=?3x2+3=?3(x+1)(x?1)(x>0),
∴h(x)在(0,1)上单调递增,在(1,+¥)上单调递减,所以h(x)=?x3+5x?3?(2x?1)的最大值为h(1)=0,
所以?x3+5x?3£2x?1,即g(x)£2x?1恒成立.
故存在这样的实常数k和m,且k=2,m=?1
略

练习册系列答案
相关题目
 ,且
,且 则不同的二次函数有( ▲ )
则不同的二次函数有( ▲ ) 上是减函数,则b的取值范围是( )
上是减函数,则b的取值范围是( )  在
在 上是增函数,则实数
上是增函数,则实数 的取值范围是
的取值范围是 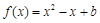 ,且
,且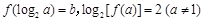 .
.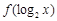 的最小值及对应的x值;
的最小值及对应的x值;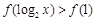 的解集记为A,不等式
的解集记为A,不等式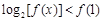 的解集记为B,求
的解集记为B,求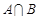 .
. .
. 表示
表示 ;
; 时,
时, 的值
的值 ,函数
,函数 ,称方程
,称方程
 的取值范围;
的取值范围; ,求
,求 的定义域为集合A,函数
的定义域为集合A,函数
 和
和 。
。 ,
, ,对于任意的
,对于任意的 都能找到
都能找到 ,使得
,使得 ,则实数
,则实数 的取值范围是 .
的取值范围是 .