题目内容
已知数列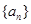 的各项均为正数,其前
的各项均为正数,其前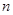 项和为
项和为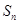 ,且
,且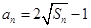 ,
,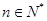 ,数列
,数列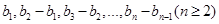 是首项和公比均为
是首项和公比均为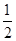 的等比数列.
的等比数列.
(1)求证数列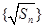 是等差数列;
是等差数列;
(2)若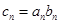 ,求数列
,求数列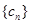 的前
的前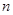 项和
项和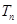 .
.
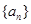 的各项均为正数,其前
的各项均为正数,其前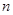 项和为
项和为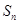 ,且
,且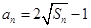 ,
,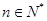 ,数列
,数列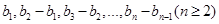 是首项和公比均为
是首项和公比均为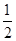 的等比数列.
的等比数列.(1)求证数列
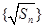 是等差数列;
是等差数列;(2)若
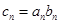 ,求数列
,求数列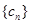 的前
的前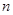 项和
项和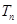 .
.(1)证明过程见试题解析(2)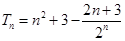
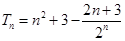
试题分析:(1)由题知
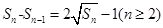 可化为
可化为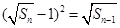 易证数列
易证数列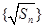 是等差数列;(2)由
是等差数列;(2)由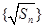 是等差数列,求出通项公式,进而求出
是等差数列,求出通项公式,进而求出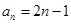 ,又据题意易求得
,又据题意易求得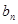 ,知
,知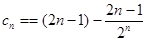 利用分组求和与错位相减法可求得前n项和
利用分组求和与错位相减法可求得前n项和 .
.试题解析:解:(1)由
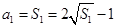 ,得
,得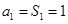 ,又
,又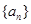 的各项均为正数,所以
的各项均为正数,所以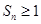 ,
,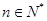 ,
,∵
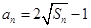 ,∴
,∴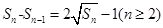 ,∴
,∴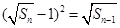 ,
,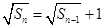 ,
,所以数列
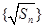 是等差数列;
是等差数列;(2)∵
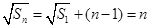 ,∴
,∴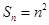 ,
,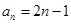 ;
;∵
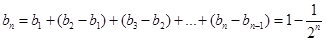 ,
,∴
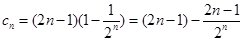 ,先求数列
,先求数列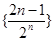 的前
的前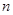 项和
项和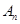 ,
,∵
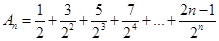 ,
,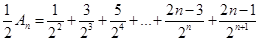 ,
,∴
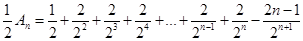 ,
,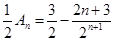 ,所以
,所以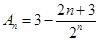 ,∴
,∴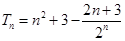 。
。
练习册系列答案
相关题目
 的前n项和为
的前n项和为 ,
,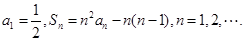
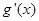 ;
;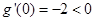 ,求证:
,求证: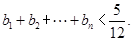
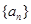 和
和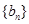 的前n项和分别为
的前n项和分别为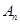 和
和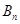 ,且
,且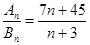 ,则使得
,则使得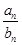 为整数的正整数n的个数是__________。
为整数的正整数n的个数是__________。 的前
的前 项和为
项和为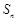 ,首项
,首项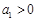 ,
,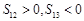 .则以下关于数列
.则以下关于数列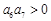 ;②
;②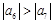 ;③
;③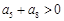 ;④前
;④前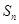 中最大的项为第六项
中最大的项为第六项 满足:
满足: ,
, ,则
,则 ( )
( )



 的前
的前 项和为
项和为 ,若
,若 ,则
,则



 中,若公差
中,若公差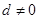 ,且
,且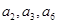 成等比数列,则公比
成等比数列,则公比 .
.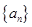 的前
的前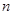 项和为
项和为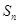 ,且4
,且4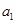 ,2
,2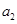 ,
,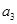 成等差数列。若
成等差数列。若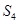 =( )
=( )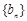 为等差数列,
为等差数列,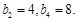 数列
数列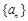 满足
满足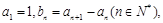 则
则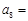 ( )
( )