题目内容
球面上有三点A、B、C,任意两点之间的球面距离都等于球大圆周长的四分之一,且过这三点的截面圆的面积为4π,则此球的体积为( )A.
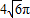
B.
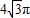
C.
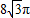
D.
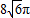
【答案】分析:因为正三角形ABC的外径r=2,故可以得到高,D是BC的中点.在△OBC中,又可以得到角以及边与R的关系,在Rt△ABD中,再利用直角三角形的勾股定理,即可解出R,最后利用体积公式求出球的体积即可.
解答:解:因为正三角形ABC的外径r=2,故高AD= r=3,D是BC的中点.
r=3,D是BC的中点.
在△OBC中,BO=CO=R,∠BOC=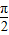 ,所以BC=BO=
,所以BC=BO=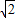 R,BD=
R,BD= BC=
BC=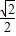 R.
R.
在Rt△ABD中,AB=BC=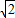 R,所以由AB2=BD2+AD2,得2R2=
R,所以由AB2=BD2+AD2,得2R2= R2+9,所以R=
R2+9,所以R=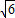 .
.
∴V=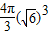 =
=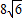
故选D.
点评:本题考查学生的空间想象能力,以及对球的性质认识及利用,球的体积和表面积是常考的题型,是基础题.
解答:解:因为正三角形ABC的外径r=2,故高AD=
 r=3,D是BC的中点.
r=3,D是BC的中点.在△OBC中,BO=CO=R,∠BOC=
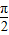 ,所以BC=BO=
,所以BC=BO=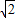 R,BD=
R,BD= BC=
BC=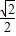 R.
R.在Rt△ABD中,AB=BC=
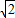 R,所以由AB2=BD2+AD2,得2R2=
R,所以由AB2=BD2+AD2,得2R2= R2+9,所以R=
R2+9,所以R=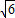 .
.∴V=
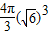 =
=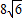
故选D.
点评:本题考查学生的空间想象能力,以及对球的性质认识及利用,球的体积和表面积是常考的题型,是基础题.

练习册系列答案
相关题目
表面积为16π的球面上有三点A、B、C,∠ACB=60°,AB=
,则球心到截面ABC的距离及B、C两点间球面距离最大值分别为( )
| 3 |
A、3,
| ||||
B、
| ||||
C、
| ||||
D、3,
|