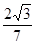题目内容
半径为1的球面上有三点A、B、C,其中AB=1,BC=
,A、C两点间的球面距离为
,则球心到平面ABC的距离为( )
| 3 |
| π |
| 2 |
分析:先确定∠BAC=
,可得球心在平面ABC内的射影为BC的中点,从而可求球心到平面ABC的距离.
| π |
| 2 |
解答:解:∵球O的半径为1,A、C两点间的球面距离为
,∴∠AOC=
∴AC=
∵AB=1,BC=
,
∴∠BAC=
∴球心在平面ABC内的射影为BC的中点
∴球心到平面ABC的距离为
=
故选B.
| π |
| 2 |
| π |
| 2 |
∴AC=
| 2 |
∵AB=1,BC=
| 3 |
∴∠BAC=
| π |
| 2 |
∴球心在平面ABC内的射影为BC的中点
∴球心到平面ABC的距离为
1-(
|
| 1 |
| 2 |
故选B.
点评:本题主要考查了球的性质,考查点面间的距离计算,属于基础题.

练习册系列答案
相关题目
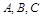 三点,其中点
三点,其中点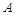 与
与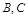 两点间的球面距离均为
两点间的球面距离均为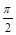 ,
,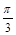 ,则球心到平面
,则球心到平面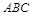 的距离为( )
的距离为( )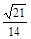 B.
B.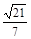 C.
C. D.
D.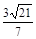
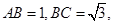 A、C两点间的球面距离为
A、C两点间的球面距离为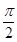 ,则球心到平面ABC的距离为
,则球心到平面ABC的距离为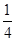 B.
B.
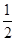 C.
C.
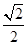 D.
D.
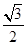
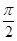 ,B
,B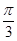 ,则过A、B、C三点的截面到球心的距离是
,则过A、B、C三点的截面到球心的距离是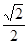 B.
B.
 C.
C.
 D.
D.