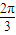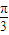题目内容
表面积为16π的球面上有三点A、B、C,∠ACB=60°,AB=
,则球心到截面ABC的距离及B、C两点间球面距离最大值分别为( )
| 3 |
A、3,
| ||||
B、
| ||||
C、
| ||||
D、3,
|
分析:设出AD,然后通过球的直径求出AD,解出∠AOB,可求A,B两点的球面距离.
解答: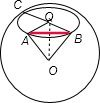 解:根据题意画出示意图,如图.
解:根据题意画出示意图,如图.
表面积为16π的球的半径R=2,
设△ABC所在小圆的半径为r,
在△ABC中,由正弦定理得:
2r=
=
=2,r=1
∴在直角三角形AOQ中,
OQ=
=
=
,
则球心到截面ABC的距离为:
;
当点C在BQ的延长线上时,B、C两点间球面距离最大,
在直角三角形BOQ中,BO=2,BQ=1,
∴∠BOQ=30°,
∴B、C两点间球面距离最大值为:∠BOC×R=
×2=
.
故选C.
 解:根据题意画出示意图,如图.
解:根据题意画出示意图,如图.表面积为16π的球的半径R=2,
设△ABC所在小圆的半径为r,
在△ABC中,由正弦定理得:
2r=
| AB |
| sin∠ACB |
| ||
| sin60° |
∴在直角三角形AOQ中,
OQ=
| OA2-AQ2 |
| 4-1 |
| 3 |
则球心到截面ABC的距离为:
| 3 |
当点C在BQ的延长线上时,B、C两点间球面距离最大,
在直角三角形BOQ中,BO=2,BQ=1,
∴∠BOQ=30°,
∴B、C两点间球面距离最大值为:∠BOC×R=
| π |
| 3 |
| 2π |
| 3 |
故选C.
点评:本题考查学生的空间想象能力,以及学生对球面上的点的距离求解,是中档题.球面上两点之间的最短连线的长度,就是经过这两点的大圆在这两点间的一段劣弧的长度.(大圆就是经过球心的平面截球面所得的圆) 我们把这个弧长叫做两点的球面距离.

练习册系列答案
相关题目
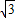 ,P为圆O1的圆周上任意一点,则M、P两点的球面距离的最值为 .
,P为圆O1的圆周上任意一点,则M、P两点的球面距离的最值为 .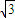 ,则球心到截面ABC的距离及B、C两点间球面距离最大值分别为( )
,则球心到截面ABC的距离及B、C两点间球面距离最大值分别为( )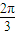
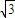 ,
,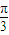
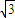 ,
,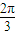
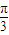
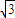 ,则球心到截面ABC的距离及B、C两点间球面距离最大值分别为( )
,则球心到截面ABC的距离及B、C两点间球面距离最大值分别为( )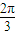
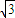 ,
,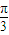
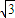 ,
,