Question

【题目】某班随机抽查了20名学生的数学成绩，分数制成如图的茎叶图，其中A组学生每天学习数学时间不足1个小时，B组学生每天学习数学时间达到一个小时。学校规定90分及90分以上记为优秀，75分及75分以上记为达标，75分以下记为未达标．

（1）分别求出A、B两组学生的平均分、并估计全班的数学平均分；

（2）现在从成绩优秀的学生中任意抽取2人，求这两人恰好都来自B组的概率；

（3）根据成绩得到如下列联表：

①直接写出表中的值；

②判断是否有的把握认为“数学成绩达标与否”与“每天学习数学时间能否达到一小时”有关．

参考公式与临界值表：K2＝.

Answer 1

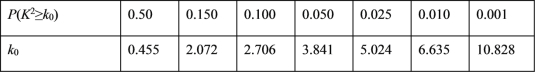
【答案】（1），，；（2）P（E）=；（3）①a=6、b=4、c=9、d=1；②没有95%的把握认为“数学成绩达标与否”与“每天学习数学时间能否达到一小时”有关

【解析】

(1)根据平均分公式分别算出A、B两组的平均分,再根据两组的平均分估算20人的总分,估算出的平均分即为估算的班级的平均分.

(2) A组优秀人数有2人,B组优秀人数有3人.列出所有可能的基本情况,利用古典概型,即可求出结果.

(3)把数据填入表格中,利用公式求得,与临界值比较即可得出结论.

（1）A组学生的平均分

B两组学生的平均分

估计全班的数学平均分

（2）设这两人恰好都来自B组为事件,由题意该概型符合古典概型,

成绩优秀的共计5人,A组2人设为,B组3人设为,

从5人中抽取两人有如下情况：

共计包含基本事件10个,事件E包含基本事件3个

两人恰好都来自B组的概率为

（3）①通过茎叶图知；

②由公式=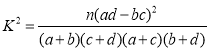

,而

所以没有的把握认为“数学成绩达标与否”与“每天学习数学时间能否达到一小时”有关.