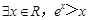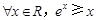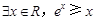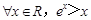题目内容
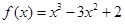 在区间
在区间 上的最大值是( )
上的最大值是( )| A.-2 | B.0 | C.2 | D.4 |
C
试题分析:由题意先对函数y进行求导,解出极值点,然后再根据函数的定义域,把极值点和区间端点值代入已知函数,判断函数在区间上的增减性,比较函数值的大小,求出最大值,从而求解
解:f'(x)=3x2-6x=3x(x-2),令f'(x)=0可得x=0或2(2舍去),当-1<x<0时,f'(x)>0,当0<x<1时,f'(x)<0,∴当x=0时,f(x)取得最大值为f(0)=2.故选C
点评:解决的关键是利用导数的符号判定函数单调性,并能结合极值得到最值,属于基础题。

练习册系列答案
相关题目
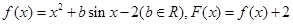 ,且对于任意实数
,且对于任意实数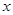 ,恒有
,恒有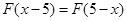 .
.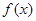 的解析式;
的解析式;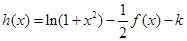 有几个零点?
有几个零点?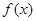 具有下列特征:
具有下列特征: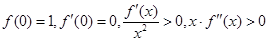 ,则
,则
 在
在 处取得极值.
处取得极值. 的值;
的值; 的方程
的方程 在区间
在区间 上恰有两个不同的实数根,求实数
上恰有两个不同的实数根,求实数 的取值范围;
的取值范围; ,不等式
,不等式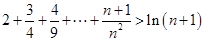 都成立.
都成立.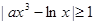 对任意
对任意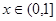 都成立,则实数a取值范围是 。
都成立,则实数a取值范围是 。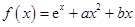 .
.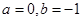 时,求
时,求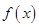 的单调区间;
的单调区间;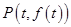
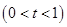 处的切线为
处的切线为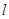 ,直线
,直线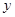 轴相交于点
轴相交于点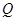 .若点
.若点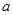 的取值范围.
的取值范围.
 ,求
,求 的单调区间;
的单调区间; ≥0时
≥0时 的取值范围.
的取值范围.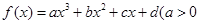 的零点的集合为{0,1},且
的零点的集合为{0,1},且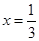 是f(x)的一个极值点。
是f(x)的一个极值点。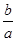 的值;
的值;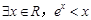 ”的否定是( )
”的否定是( )