Question

【题目】如图，AB是平面的斜线段，A为斜足，点C满足，且在平面内运动，则有以下几个命题：

①当时，点C的轨迹是抛物线；

②当时，点C的轨迹是一条直线；

③当时，点C的轨迹是圆；

④当时，点C的轨迹是椭圆；

⑤当时，点C的轨迹是双曲线.

其中正确的命题是__________.（将所有正确的命题序号填到横线上）

Answer 1

【答案】②③

【解析】

根据题意，分别验证和时C点的轨迹，当时，作斜线段AB的中垂面，与平面的交线为一条直线，即为C点轨迹；当时，作B在平面内的射影为D，

连接BD，CD，在平面内建立平面直角坐标系，求C点轨迹方程，根据轨迹方程即可判断.

当时，，过AB的中点作线段AB的垂面，

则点C在与的交线上，即点C的轨迹是一条直线；

当时，，设B在平面内的射影为D，

连接BD，CD，

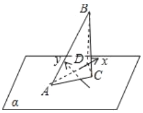
设，，则，

在平面内，以AD所在直线为x轴，以AD的中垂线为y轴如图建立平面直角坐标系，

设，则有

则，，

，

∴，

化简可得.

∴C的轨迹是圆.

故答案为：②③