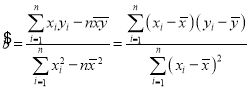题目内容
【题目】如果存在常数k使得无穷数列![]() 满足
满足![]() 恒成立,则称为
恒成立,则称为![]() 数列.
数列.
(1)若数列![]() 是
是![]() 数列,
数列,![]() ,
,![]() ,求
,求![]() ;
;
(2)若等差数列![]() 是
是![]() 数列,求数列
数列,求数列![]() 的通项公式;
的通项公式;
(3)是否存在![]() 数列
数列![]() ,使得
,使得![]() ,
,![]() ,
,![]() ,…是等比数列?若存在,请求出所有满足条件的数列
,…是等比数列?若存在,请求出所有满足条件的数列![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() 或
或![]() ;(3)存在;满足条件的
;(3)存在;满足条件的![]() 数列
数列![]() 有无穷多个,其通项公式为
有无穷多个,其通项公式为![]() .
.
【解析】
(1)根据![]() 数列的定义,得
数列的定义,得![]() ,
,![]() ,可求
,可求![]() ;
;
(2)根据![]() 数列的定义,得
数列的定义,得![]() ,分
,分![]() 和
和![]() 两种情况讨论. 当
两种情况讨论. 当![]() ,
,![]() .当
.当![]() 时,由
时,由![]() 是等差数列,对
是等差数列,对![]() 赋值,求出
赋值,求出![]() 和公差
和公差![]() ,即求
,即求![]() ;
;
(3)假设存在满足条件的![]() 数列
数列![]() ,设等比数列
,设等比数列![]() ,
,![]() ,
,![]() ,…的公比为q.则有
,…的公比为q.则有![]() ,
,![]() ,可得q=1,故当
,可得q=1,故当![]() 时,
时,![]() .当
.当![]() 时,不妨设
时,不妨设![]() ,
,![]() 且i为奇数,
且i为奇数,
由![]() ,可得
,可得![]() .
.
即满足条件的![]() 数列
数列![]() 有无穷多个,其通项公式为
有无穷多个,其通项公式为![]() .
.
(1)由数列![]() 是
是![]() 数列,得
数列,得![]() ,
,![]() ,可得
,可得![]() ;
;
(2)由![]() 是
是![]() 数列知
数列知![]() 恒成立,取m=1得
恒成立,取m=1得![]() 恒成立,
恒成立,
当![]() ,
,![]() 时满足题意,此时
时满足题意,此时![]() ,
,
当![]() 时,由
时,由![]() 可得
可得![]() ,取m=n=2得
,取m=n=2得![]() ,
,
设公差为d,则![]() 解得
解得![]() 或者
或者![]() ,
,
综上,![]() 或
或![]() 或
或![]() ,经检验均合题意.
,经检验均合题意.
(3)假设存在满足条件的![]() 数列
数列![]() ,
,
不妨设该等比数列![]() ,
,![]() ,
,![]() ,…的公比为q,
,…的公比为q,
则有![]() ,
,
可得![]() ①
①
![]() ,
,
可得![]() ②
②
综上①②可得q=1,
故![]() ,代入
,代入![]() 得
得![]() ,
,
则当![]() 时,
时,![]() ,
,
又![]() ,
,
当![]() 时,不妨设
时,不妨设![]() ,
,![]() 且i为奇数,
且i为奇数,
由![]() ,
,
而![]() ,
,![]() ,
,![]() ,
,![]() .
.
综上,满足条件的![]() 数列
数列![]() 有无穷多个,其通项公式为
有无穷多个,其通项公式为![]() .
.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案【题目】随着经济的快速增长、规模的迅速扩张以及人民生活水平的逐渐提高,日益剧增的垃圾给城市的绿色发展带来了巨大的压力.相关部门在有5万居民的光明社区采用分层抽样方法得到年内家庭人均![]() 与人均垃圾清运量的统计数据如下表:
与人均垃圾清运量的统计数据如下表:
人均 | 3 | 6 | 9 | 12 | 15 |
人均垃圾清运量 | 0.13 | 0.23 | 0.31 | 0.41 | 0.52 |
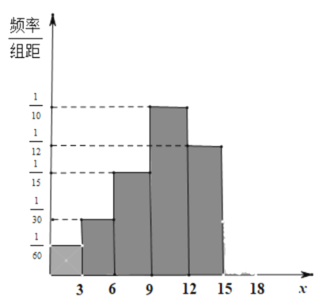
(1)已知变量![]() 与
与![]() 之间存在线性相关关系,求出其回归直线方程;
之间存在线性相关关系,求出其回归直线方程;
(2)随着垃圾分类的推进,燃烧垃圾发电的热值大幅上升,平均每吨垃圾可折算成上网电量200千瓦时,如图是光明社区年内家庭人均![]() 的频率分布直方图,请补全
的频率分布直方图,请补全![]() 的缺失部分,并利用(1)的结果,估计整个光明社区年内垃圾可折算成的总上网电量.
的缺失部分,并利用(1)的结果,估计整个光明社区年内垃圾可折算成的总上网电量.
参考公式]回归方程![]() ,
,