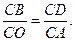题目内容
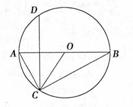
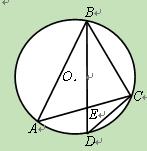
如图,A,B,C,D四点在同一圆上,AD的延长线与BC的延长线交于E点,且EC=ED.
(I)证明:CD//AB;
(II)延长CD到F,延长DC到G,使得EF=EG,证明:A,B,G,F四点共圆.
解: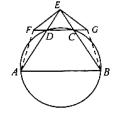
(I)因为EC=ED,所以∠EDC=∠ECD.
因为A,B,C,D四点在同一圆上,所以∠EDC=∠EBA.故∠ECD=∠EBA,所以CD//AB.…5分
(II)由(I)知,AE=BE,因为EF=FG,故∠EFD=∠EGC
从而∠FED=∠GEC.连结AF,BG,则△EFA≌△EGB,故∠FAE=∠GBE,
又CD//AB,∠EDC=∠ECD,所以∠FAB=∠GBA.
所以∠AFG+∠GBA=180°.故A,B,G,F四点共圆
解析

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
直线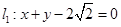 与直线
与直线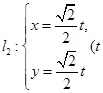 为参数)的交点到原点O的距离是( )
为参数)的交点到原点O的距离是( )
| A.1 | B.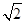 | C.2 | D.2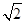 |

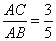 ,求
,求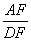 的值.
的值. 与圆
与圆 相切于点
相切于点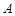 ,经过点
,经过点 交圆
交圆 ,
, 的平分线分别交
的平分线分别交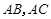 于点
于点 .
.
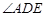 =
=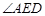 ;
; ,求
,求 的值.
的值.
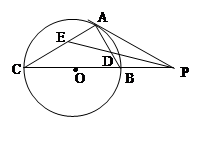
 相交于A、B两点,AB是
相交于A、B两点,AB是 的直径,过A点作
的直径,过A点作 的切线交
的切线交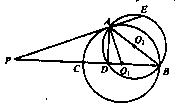
 的外接圆,D
的外接圆,D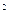 =DE·DB;
=DE·DB;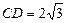 ,O到AC的距离为1,求⊙O的半径
,O到AC的距离为1,求⊙O的半径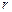 .
.
 为⊙
为⊙ 的直径,
的直径, 切⊙
切⊙ ,
, 交⊙
交⊙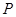 ,
,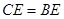 ,点
,点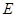 在
在 是⊙
是⊙