题目内容
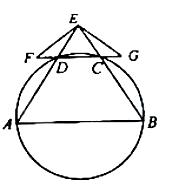
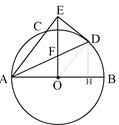
如图,AB是⊙O的直径 ,AC是弦 ,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E.OE交AD于点F.
(Ⅰ)求证:DE是⊙O的切线;
(Ⅱ)若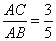 ,求
,求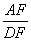 的值.
的值.
(Ⅰ)先证DE⊥OD (Ⅱ)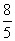
解析试题分析:(1)连结OD,可得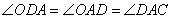
∴OD∥AE 又AE⊥DE ∴DE⊥OD,又OD为半径,∴DE是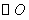 的切线
的切线
(2)过D作DH⊥AB于H,则有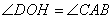
Cos∠DOH=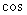 ∠CAB=
∠CAB=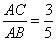
设OD=5x,则AB=10x,OH=3x,DH=4x ∴AH=8x AD2=80x2
由△AED∽△ADB可得 AD2=AE·AB=AE·10x ∴AE=8X
又由△AEF∽△DOF 可得AF∶DF= AE∶OD =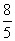 ;∴
;∴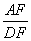 =
=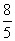
考点:切线的判定与性质;角平分线的定义;平行线的性质;等腰三角形的性质;勾股定理;圆周角定理;相似三角形的判定与性质;锐角三角函数的定义.
点评:本题综合考查了等腰三角形的性质,平行线的性质,切线的性质和判定,相似三角形的性质和判定,锐角三角函数,勾股定理,角平分线定义等知识点的运用,题目较好,综合性强,有一定的难度,主要培养学生综合运用所学知识进行推理的能力.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 中,
中,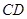 是
是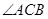 的角平分线,
的角平分线,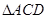 的外接圆交
的外接圆交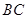 于
于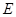 ,
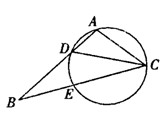
,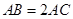 .
.
 ;
;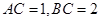 时,求
时,求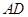 的长.
的长.
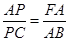 ;
;  的值.
的值.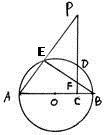
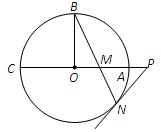
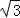 ,OA=
,OA=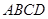 是☉
是☉ 的内接四边形,
的内接四边形, 不经过点
不经过点 平分
平分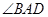 ,经过点
,经过点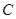 的直线分别交
的直线分别交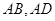 的延长线于点
的延长线于点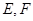 ,且
,且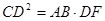 ,证明:
,证明: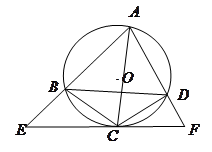
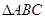 ∽
∽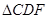 ;
; 是☉
是☉ 的三个顶点都在⊙O上,
的三个顶点都在⊙O上, 的平分线与BC边和⊙O分别交于点D、E.
的平分线与BC边和⊙O分别交于点D、E.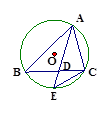
 ,求
,求 的长.
的长. ,PD=1,BD=8,求线段BC的长.
,PD=1,BD=8,求线段BC的长.