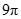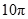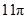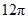题目内容
在空间四边形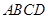 中,
中,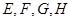 分别是
分别是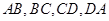 的中点。若
的中点。若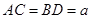 ,且
,且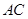 与
与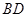 所成的角为
所成的角为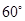 ,则四边形
,则四边形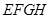 的面积为( )
的面积为( )
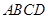 中,
中,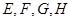 分别是
分别是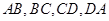 的中点。若
的中点。若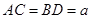 ,且
,且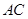 与
与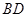 所成的角为
所成的角为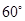 ,则四边形
,则四边形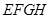 的面积为( )
的面积为( )A.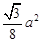 | B.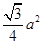 | C.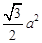 | D.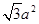 |
A
试题分析:连接EH,因为EH是△ABD的中位线,所以EH∥BD,且EH=BD.
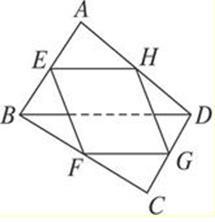
同理,FG∥BD,EF∥AC,且FG=BD,EF=AC.
所以EH∥FG,且EH=FG.
所以四边形EFGH为平行四边形.
因为AC=BD=a,AC与BD所成的角为60°
所以EF=EH.所以四边形EFGH为菱形,∠EFG=60°.
∴四边形EFGH的面积是2×
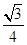 ×(
×(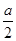 )2=
)2=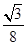 a2
a2故答案为:
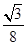 a2选A.
a2选A.点评:解决该试题的关键是先证明四边形EFGH为菱形,然后说明∠EFG=60°,最后根据三角形的面积公式即可求出所求.

练习册系列答案
相关题目
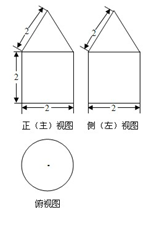
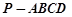 的三视图如右图所示,四棱锥
的三视图如右图所示,四棱锥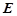 、
、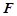 分别是棱
分别是棱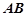 、
、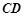 的中点,直线
的中点,直线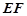 被球面所截得的线段长为
被球面所截得的线段长为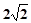 ,则该球表面积为 .
,则该球表面积为 .
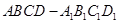 的棱长为1,线段
的棱长为1,线段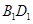 上有两个动点E,F,且
上有两个动点E,F,且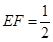 ,则下列结论中错误的是 ( )
,则下列结论中错误的是 ( )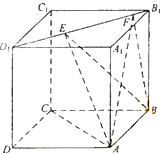
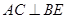

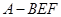 的体积为定值
的体积为定值
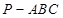 中,底面
中,底面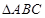 是边长为2的正三角形,
是边长为2的正三角形,  ⊥底面
⊥底面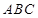 ,且
,且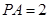 ,则此三棱锥外接球的半径为( )
,则此三棱锥外接球的半径为( )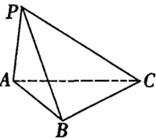

 的边
的边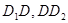 的中点,沿SE、SF、EF将它折成一个几何体,使
的中点,沿SE、SF、EF将它折成一个几何体,使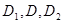 重合,记作D,给出下列位置关系:①SD
重合,记作D,给出下列位置关系:①SD 面EFD ; ②SE
面EFD ; ②SE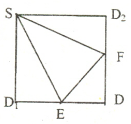
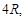 高为
高为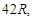 则它最多能放入半径为
则它最多能放入半径为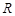 的球 个。
的球 个。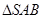 与直角梯形
与直角梯形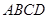 垂直,
垂直,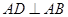 ,
,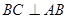 ,
,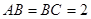 ,
,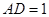 .若
.若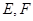 分别为
分别为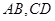 的中点.
的中点.
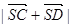 的值; (2)求面
的值; (2)求面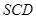 与面
与面 所成的二面角大小.
所成的二面角大小.