题目内容
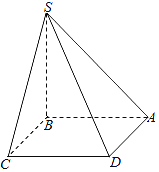
【题目】如图,在三棱台![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的等边三角形,上、下底面的面积之比为
的等边三角形,上、下底面的面积之比为![]() ,侧面
,侧面![]() 底面
底面![]() ,并且
,并且![]() .
.
(1)平面![]() 平面
平面![]() ,证明:
,证明:![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成二面角的正弦值.
所成二面角的正弦值.
【答案】(1)见证明;(2)![]()
【解析】
(1)由题意可知![]() ,结合几何关系可证得
,结合几何关系可证得![]() 平面
平面![]() ,据此可得题中的结论;
,据此可得题中的结论;
(2)以![]() 为原点建立空间直角坐标系.由题意求得平面
为原点建立空间直角坐标系.由题意求得平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,据此求解平面
,据此求解平面![]() 与平面
与平面![]() 所成二面角的正弦值即可.
所成二面角的正弦值即可.
(1)![]() 几何体
几何体![]() 为棱台,
为棱台,
![]() 平面
平面![]() 平面
平面![]()
![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
(2)![]() ,则面积之比为相似比的平方,
,则面积之比为相似比的平方,![]() 而
而![]()
![]() 过点
过点![]() 作
作![]() 交
交![]() 于
于![]() ,由于侧面
,由于侧面![]() 底面
底面![]() 为交线,
为交线,![]() 底面
底面![]() .在
.在![]() 中,易求得
中,易求得![]() 为线段
为线段![]() 的四等分点,取
的四等分点,取![]() 的中点
的中点![]() ,则有
,则有![]() ,以
,以![]() 为原点建立空间直角坐标系.
为原点建立空间直角坐标系.
![]()
![]()
![]()
![]()
设平面![]() 的法向量为
的法向量为![]()
 可得
可得![]()
设平面![]() 的法向量为
的法向量为![]()
![]()
故平面![]() 与平面
与平面![]() 所成二面角的正弦值为
所成二面角的正弦值为![]() .
.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
【题目】艾滋病是一种危害性极大的传染病,由感染艾滋病病毒![]() 病毒
病毒![]() 引起,它把人体免疫系统中最重要的CD4T淋巴细胞作为主要攻击目标,使人体丧失免疫功能
引起,它把人体免疫系统中最重要的CD4T淋巴细胞作为主要攻击目标,使人体丧失免疫功能![]() 下表是近八年来我国艾滋病病毒感染人数统计表:
下表是近八年来我国艾滋病病毒感染人数统计表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代码x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
感染者人数 |
|
|
|
|
|
|
| 85 |
![]() 请根据该统计表,画出这八年我国艾滋病病毒感染人数的折线图;
请根据该统计表,画出这八年我国艾滋病病毒感染人数的折线图;
![]() 请用相关系数说明:能用线性回归模型拟合y与x的关系;
请用相关系数说明:能用线性回归模型拟合y与x的关系;
![]() 建立y关于x的回归方程
建立y关于x的回归方程![]() 系数精确到
系数精确到![]() ,预测2019年我国艾滋病病毒感染人数.
,预测2019年我国艾滋病病毒感染人数.
参考数据:![]() ;
;![]() ,
,![]() ,
,![]() ,
,
参考公式:相关系数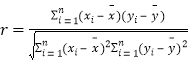 ,
,
回归方程![]() 中,
中,![]()
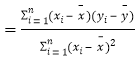 ,
,![]() .
.