题目内容
【题目】如图,四棱锥S-ABCD的底面是边长为1的正方形,则棱SB垂直于底面.
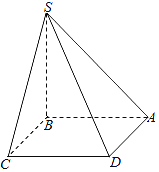
(1)求证:平面SBD⊥平面SAC;
(2)若SA与平面SCD所成角的正弦值为![]() ,求SB的长.
,求SB的长.
【答案】(1)证明见解析;(2) 2或![]() .
.
【解析】
(1)连结AC,BD,证明AC⊥BD,AC⊥SB,得出AC⊥面SBD,即可证明平面SAC⊥平面SBD;
(2)将四棱锥补成正四棱柱ABCD-A′SC′D′,连结A′D,作AE⊥A′D于E,连结SE,
证明AE⊥面SCD,得出∠ASE为SA与平面SCD所成角的平面角,利用直角三角形的边角关系求出SB的长.
(1)证明:连结AC,BD,如图所示;
∵四边形ABCD是正方形,∴AC⊥BD,
∵SB⊥底面ABCD,∴AC⊥SB,
∴AC⊥面SBD,
又由AC面SAC,∴面SAC⊥面SBD.
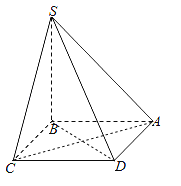
(2)解:将四棱锥补成正四棱柱ABCD-A′SC′D′,
连结A′D,作AE⊥A′D于E,连结SE,如图所示;
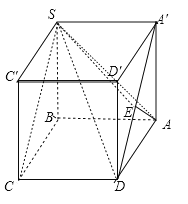
由SA′∥CD,知平面SCD即为平面SCDA′,
∵CD⊥侧面ADD′A′,∴CD⊥AE,
又AE⊥A′D,∴AE⊥面SCD,
∴∠ASE即为SA与平面SCD所成角的平面角,
设SB=x,
在直角△ABS中,由勾股定理得SA=![]() ;
;
在直角△SAE中,![]() =
=![]() ,得AE=
,得AE=![]() ;
;
在直角△DAA′中,A′DAE=ADAA′,
即![]()
![]() =1x;
=1x;
解得x=2或x=![]() ;
;
∴SB的长为2或![]() .
.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
【题目】上海市普通高中学业水平等级考成绩共分为五等十一级,各等级换算成分数如表所示:
等级 |
| A |
| B |
|
| C |
|
| D | E |
分数 | 70 | 67 | 64 | 61 | 58 | 55 | 52 | 49 | 46 | 43 | 40 |
上海某高中2018届高三![]() 班选考物理学业水平等级考的学生中,有5人取得
班选考物理学业水平等级考的学生中,有5人取得![]() 成绩,其他人的成绩至少是B级及以上,平均分是64分,这个班级选考物理学业水平等级考的人数至少为______人
成绩,其他人的成绩至少是B级及以上,平均分是64分,这个班级选考物理学业水平等级考的人数至少为______人![]()