题目内容
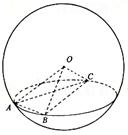
如图，A、B、C是表面积为48π的球面上三点，AB=2，BC=4，∠ABC=60º，O为球心，则直线OA与截面ABC所成的角是（ ）
A．arcsin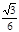
B．arccos 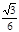C．arcsin
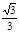D．arccos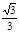
A．arcsin
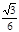B．arccos 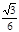C．arcsin 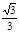D．arccos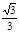D
解：设O在截面ABC上的射影是O1，
则O1为截面三角形ABC的外心，连接AO1，
则∠OAO1为直线OA与截面ABC所成的角．
球的半径为R，小圆半径为r．
由球的表面积为48π，得R="2"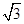
，
在△ABC中，有余弦定理得AC2=AB2+BC2-2AB•BC•cos∠ABC=4+16-16cos60°=12⇒AC=2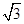
由正弦定理得AC: sin∠ABC =4=2r，即r=2．
∴cos∠OAO1="O" 1A: OA ="r" :R =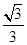
．
∴直线OA与截面ABC所成的角是：arccos ．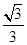
故答案为D
则O1为截面三角形ABC的外心，连接AO1，
则∠OAO1为直线OA与截面ABC所成的角．
球的半径为R，小圆半径为r．
由球的表面积为48π，得R="2"
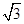，在△ABC中，有余弦定理得AC2=AB2+BC2-2AB•BC•cos∠ABC=4+16-16cos60°=12⇒AC=2
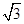
由正弦定理得AC: sin∠ABC =4=2r，即r=2．
∴cos∠OAO1="O" 1A: OA ="r" :R =
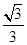．∴直线OA与截面ABC所成的角是：arccos
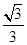．故答案为D
练习册系列答案
相关题目
中，底面
是直角梯形，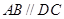
，
，
，
，
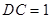平面
．
平面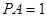
；
平面
； 
是
的中点，求三棱锥
的体积．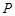
出发的三条射线
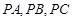两两成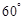
角，且分别与球
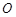相切于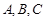
三点，若球的体积为
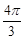，则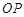
两点之间的距离为( )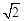 
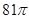
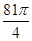
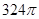
中，
∠
，
=∠
，则
等于（ ）
、
、
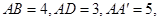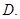
，则这个长方体的外接球的表面积为 .