题目内容
5.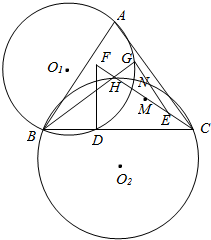 H为锐角三角形ABC的垂心,在线段CH上任取一点E,延长CH到F,使HF=CE,作FD⊥BC,EG⊥BH,其中D,G为垂足,M是线段CF的中点,O1,O2分别△ABG,△BCH的外接圆圆心,⊙O1,⊙O2的另一交点为N;证明:
H为锐角三角形ABC的垂心,在线段CH上任取一点E,延长CH到F,使HF=CE,作FD⊥BC,EG⊥BH,其中D,G为垂足,M是线段CF的中点,O1,O2分别△ABG,△BCH的外接圆圆心,⊙O1,⊙O2的另一交点为N;证明:(1)A,B,D,G四点共圆;
(2)O1,O2,M,N四点共圆.
分析 (1)设EG∩DF=K,连接AH,可得△CAH≌△EKF,进而AH与KF平行且相等,进而∠KAB=90°=∠KDB=∠KGB,故A,B,D,G四点共圆;
(2)由(1)得:BK为圆O1的直径,作圆O2的直径BP,连接CP,KP,HP,O1O2,可得O1,O2,M分别是△KBP三边的中点,进而可得四边形O1O2MN为梯形,故O1,O2,M,N四点共圆.
解答 证明:(1)如图,设EG∩DF=K,连接AH,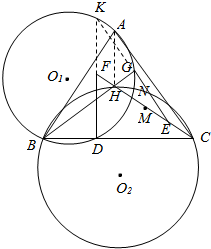
∵AC⊥BH,EK⊥BH,AH⊥BC,KF⊥BC,
∴AC∥EK,AH∥KF,且CH=EF,
∴△CAH≌△EKF,
∴AH与KF平行且相等,
故AK∥HF,
∴∠KAB=90°=∠KDB=∠KGB,
∴A,B,D,G四点共圆;
(2)由(1)得:BK为圆O1的直径,作圆O2的直径BP,连接CP,KP,HP,O1O2,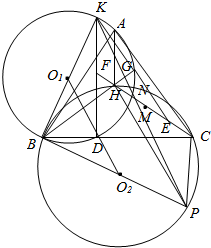
则∠BCP=∠BHP=90°,
∴CP∥AH,HP∥AC,
故AHPC为平行四边形,
进而PC=KF,且PC∥KF,
故KP与CF互相平分于M,
故O1,O2,M分别是△KBP三边的中点,
∴KM∥O1O2,
而由∠KNB=90°,O1O2⊥KN,
∴N,M,K三点共线,
∴MN∥O1O2,
根据三角形中位线定理可得:
MO2=O1B=O1N,
因此四边形O1O2MN为梯形.
故O1,O2,M,N四点共圆.
点评 本题考查的知识点是圆内接四边形的性质与判定,本题辅助线添加比较难想到,而且转化困难,属于难题.

练习册系列答案
相关题目
16.P是双曲线$\frac{x^2}{16}-\frac{y^2}{20}=1$上一点,F1,F2分别是双曲线左右焦点,若|PF1|=9,则|PF2|=( )
| A. | 1 | B. | 17 | C. | 1或17 | D. | 以上答案均不对 |
20.行如图所示的程序框图,若输入a=390,b=156,则输出a=( )
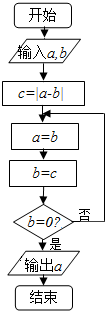

| A. | 26 | B. | 39 | C. | 78 | D. | 156 |
14.已知集合M={x|x>1},N={x|-3<x<2},则集合M∩N等于( )
| A. | {x|-3<x<2} | B. | {x|-3<x<1} | C. | {x|1<x<2} | D. | {x|2<x<3} |
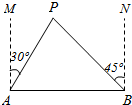 如图,A、B两座城市相距100千米,现计划在这两座城市之间修筑一条高等级公路(即线段AB).经测量,森林保护区中心P点在A城市的北偏东30°方向,B城市的北偏西45°方向上,已知森林保护区的范围在以P为圆心,50千米为半径的圆形区域内.请问:计划修筑的这条高等级公路会不会穿越保护区,为什么?
如图,A、B两座城市相距100千米,现计划在这两座城市之间修筑一条高等级公路(即线段AB).经测量,森林保护区中心P点在A城市的北偏东30°方向,B城市的北偏西45°方向上,已知森林保护区的范围在以P为圆心,50千米为半径的圆形区域内.请问:计划修筑的这条高等级公路会不会穿越保护区,为什么?