题目内容
14.已知集合M={x|x>1},N={x|-3<x<2},则集合M∩N等于( )| A. | {x|-3<x<2} | B. | {x|-3<x<1} | C. | {x|1<x<2} | D. | {x|2<x<3} |
分析 由M与N,求出两集合的交集即可.
解答 解:∵M={x|x>1},N={x|-3<x<2},
∴M∩N={x|1<x<2},
故选:C.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
4.如图是某算法的程序框图,若输出的b值为32,则判断框内①应填( )

| A. | 4? | B. | 5? | C. | 6? | D. | 7? |
9.已知函数f(x)=$\left\{{\begin{array}{l}{{{log}_2}x+a,x>0}\\{{2^x}+a,x≤0}\end{array}}$,若函数y=f(x)+x有且只有一个零点,则实数a的取值范围是( )
| A. | (-∞,-1] | B. | (-∞,-1) | C. | (-1,+∞) | D. | [-1,+∞) |
19.定义在R上的函数g(x)=ex+e-x+|x|,则满足g(2x-1)<g(3)的x的取值范围是( )
| A. | (-∞,2) | B. | (-2,2) | C. | (-1,2) | D. | (2,+∞) |
4.等差数列{an}中,a1+a3+a5=π,则cosa3=( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
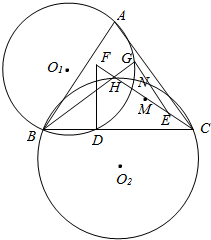 H为锐角三角形ABC的垂心,在线段CH上任取一点E,延长CH到F,使HF=CE,作FD⊥BC,EG⊥BH,其中D,G为垂足,M是线段CF的中点,O1,O2分别△ABG,△BCH的外接圆圆心,⊙O1,⊙O2的另一交点为N;证明:
H为锐角三角形ABC的垂心,在线段CH上任取一点E,延长CH到F,使HF=CE,作FD⊥BC,EG⊥BH,其中D,G为垂足,M是线段CF的中点,O1,O2分别△ABG,△BCH的外接圆圆心,⊙O1,⊙O2的另一交点为N;证明: