题目内容
10.已知等差数列{an}中,等式(m-n)am+n=mam-nan(m、n∈N*)恒成立,运用类比思想方法,可知在等比数列{bn}中,与此类似的等式bm+n=bm$(\frac{{b}_{n}}{{b}_{m}})^{\frac{n}{n-m}}$恒成立.分析 bn=b1qn-1,bm=b1qm-1,可得qn-m=$\frac{{b}_{n}}{{b}_{m}}$,q=$(\frac{{b}_{n}}{{b}_{m}})^{\frac{1}{n-m}}$,利用bm+n=bmqn,可得结论.
解答 解:∵bn=b1qn-1,bm=b1qm-1,
∴qn-m=$\frac{{b}_{n}}{{b}_{m}}$,
∴q=$(\frac{{b}_{n}}{{b}_{m}})^{\frac{1}{n-m}}$
∴bm+n=bmqn=bm$(\frac{{b}_{n}}{{b}_{m}})^{\frac{n}{n-m}}$.
故答案为:bm+n=bm$(\frac{{b}_{n}}{{b}_{m}})^{\frac{n}{n-m}}$.
点评 本题考查类比思想,考查等比数列的通项的性质,考查学生分析解决问题的能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.已知等差数列{an}前四项中第二项为606,前四项和Sn为2600,则第4项为( )
| A. | 707 | B. | 782 | C. | 870 | D. | 990 |
15.设m、n是不同的直线,α、β是不同的平面,有以下四个命题:
①若m⊥n,m⊥α,则n∥α
②若n⊥β,m∥α,α⊥β,则m∥n
③若m⊥α,m∥β,则α⊥β
④若m∥n,n?α,则m∥α
其中真命题的个数是( )
①若m⊥n,m⊥α,则n∥α
②若n⊥β,m∥α,α⊥β,则m∥n
③若m⊥α,m∥β,则α⊥β
④若m∥n,n?α,则m∥α
其中真命题的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
19.定义在R上的函数g(x)=ex+e-x+|x|,则满足g(2x-1)<g(3)的x的取值范围是( )
| A. | (-∞,2) | B. | (-2,2) | C. | (-1,2) | D. | (2,+∞) |
20.若圆x2+y2+2kx+2y+2=0(k>0)与两坐标轴无公共点,那么实数k的取值范围是( )
| A. | 0<k<$\sqrt{2}$ | B. | 1<k<$\sqrt{2}$ | C. | 0<k<1 | D. | k>$\sqrt{2}$ |
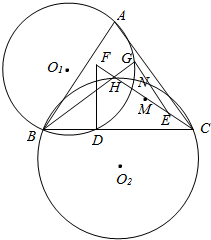 H为锐角三角形ABC的垂心,在线段CH上任取一点E,延长CH到F,使HF=CE,作FD⊥BC,EG⊥BH,其中D,G为垂足,M是线段CF的中点,O1,O2分别△ABG,△BCH的外接圆圆心,⊙O1,⊙O2的另一交点为N;证明:
H为锐角三角形ABC的垂心,在线段CH上任取一点E,延长CH到F,使HF=CE,作FD⊥BC,EG⊥BH,其中D,G为垂足,M是线段CF的中点,O1,O2分别△ABG,△BCH的外接圆圆心,⊙O1,⊙O2的另一交点为N;证明: