题目内容
15.定义运算:$\overrightarrow{a}$?$\overrightarrow{b}$=|$\overrightarrow{a}$||$\overrightarrow{b}$|sinθ,其中θ为向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角,若向量$\overrightarrow{m}$,$\overrightarrow{n}$满足|$\overrightarrow{m}$|=1,|$\overrightarrow{n}$|=2,$\overrightarrow{m}•\overrightarrow{n}$=-1,则|$\overrightarrow{m}$?$\overrightarrow{n}$|的值为$\sqrt{3}$.分析 由条件利用两个向量的数量积的定义求得cosθ 的值,可得 θ 的值,从而求得|$\overrightarrow{m}$?$\overrightarrow{n}$|的值.
解答 解:向量$\overrightarrow{m}$,$\overrightarrow{n}$满足|$\overrightarrow{m}$|=1,|$\overrightarrow{n}$|=2,$\overrightarrow{m}•\overrightarrow{n}$=1×2×cosθ=-1,
∴cosθ=-$\frac{1}{2}$,∴θ=120°,
则|$\overrightarrow{m}$?$\overrightarrow{n}$|=1×2×sin120°=$\sqrt{3}$,
故答案为:$\sqrt{3}$.
点评 本题主要考查新定义,两个向量的数量积的定义,属于基础题.

练习册系列答案
相关题目
10.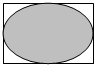 如图中,矩形长为6,宽为4,向矩形内随机掷300颗黄豆,数得落在椭圆内的黄豆数204,则一次实验数据为依据估计出椭圆的面积约为( )
如图中,矩形长为6,宽为4,向矩形内随机掷300颗黄豆,数得落在椭圆内的黄豆数204,则一次实验数据为依据估计出椭圆的面积约为( )
 如图中,矩形长为6,宽为4,向矩形内随机掷300颗黄豆,数得落在椭圆内的黄豆数204,则一次实验数据为依据估计出椭圆的面积约为( )
如图中,矩形长为6,宽为4,向矩形内随机掷300颗黄豆,数得落在椭圆内的黄豆数204,则一次实验数据为依据估计出椭圆的面积约为( )| A. | 7.66 | B. | 16.32 | C. | 17.28 | D. | 8.68 |
20.若圆x2+y2+2kx+2y+2=0(k>0)与两坐标轴无公共点,那么实数k的取值范围是( )
| A. | 0<k<$\sqrt{2}$ | B. | 1<k<$\sqrt{2}$ | C. | 0<k<1 | D. | k>$\sqrt{2}$ |
4.等差数列{an}中,a1+a3+a5=π,则cosa3=( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
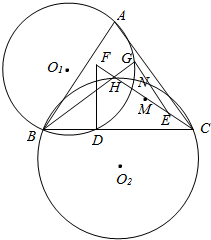 H为锐角三角形ABC的垂心,在线段CH上任取一点E,延长CH到F,使HF=CE,作FD⊥BC,EG⊥BH,其中D,G为垂足,M是线段CF的中点,O1,O2分别△ABG,△BCH的外接圆圆心,⊙O1,⊙O2的另一交点为N;证明:
H为锐角三角形ABC的垂心,在线段CH上任取一点E,延长CH到F,使HF=CE,作FD⊥BC,EG⊥BH,其中D,G为垂足,M是线段CF的中点,O1,O2分别△ABG,△BCH的外接圆圆心,⊙O1,⊙O2的另一交点为N;证明: