题目内容
6.(x$\sqrt{x}$+$\frac{1}{{x}^{4}}$)n的展开式中,第3项的二项式系数比第2项的二项式系数大44,则展开式中的常数项是第4项.分析 在二项展开式的通项公式中,令x的幂指数等于0,求出r的值,即可求得展开式中的常数项.
解答 解:由题意可得,Cn2-Cn1=44,可求n=11,故(x$\sqrt{x}$+$\frac{1}{{x}^{4}}$)n的展开式的通项公式为Tr+1=${C}_{11}^{r}$•${x}^{\frac{33-11r}{2}}$,
令 $\frac{33-11r}{2}$=0,求得r=3,可得展开式中的常数项是第第四项,
故答案为:4.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
18.下列命题中,正确的是( )
| A. | 若a>b,则ac>bc | B. | 若a>b,则ac2>bc2 | ||
| C. | 若a>b,则an>bn(n∈N*) | D. | 若a>b,c<d,则a-c>b-d |
15.某程序框图如图所示,该程序运行后输出的S的值是( )
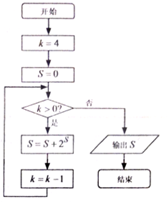

| A. | 2059 | B. | 1035 | C. | 11 | D. | 3 |