题目内容
【题目】已知数列![]() 的各项均为整数,其前n项和为
的各项均为整数,其前n项和为![]() .规定:若数列
.规定:若数列![]() 满足前r项依次成公差为1的等差数列,从第
满足前r项依次成公差为1的等差数列,从第![]() 项起往后依次成公比为2的等比数列,则称数列
项起往后依次成公比为2的等比数列,则称数列![]() 为“r关联数列”.
为“r关联数列”.
(1)若数列![]() 为“6关联数列”,求数列
为“6关联数列”,求数列![]() 的通项公式;
的通项公式;
(2)在(1)的条件下,求出![]() ,并证明:对任意
,并证明:对任意![]() ,
,![]() ;
;
(3)若数列![]() 为“6关联数列”,当
为“6关联数列”,当![]() 时,在
时,在![]() 与
与![]() 之间插入n个数,使这
之间插入n个数,使这![]() 个数组成一个公差为
个数组成一个公差为![]() 的等差数列,求
的等差数列,求![]() ,并探究在数列
,并探究在数列![]() 中是否存在三项
中是否存在三项![]() ,
,![]() ,
,![]() 其中m,k,p成等差数列)成等比数列?若存在,求出这样的三项;若不存在,说明理由.
其中m,k,p成等差数列)成等比数列?若存在,求出这样的三项;若不存在,说明理由.
【答案】(1)![]()
(2)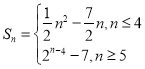 ,证明见解析
,证明见解析
(3)![]() ,不存在,理由见解析
,不存在,理由见解析
【解析】
(1)根据题意得到![]() ,
,![]() ,且
,且![]() .解得
.解得![]() 即可求出
即可求出![]() 的通项公式.
的通项公式.
(2)由(1)得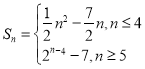 ,利用换元法证明数列
,利用换元法证明数列![]() 的最小项为
的最小项为![]() ,即可证明对任意
,即可证明对任意![]() ,
,![]() .
.
(3)由(1)可知,当![]() 时,
时,![]() ,由此可得出
,由此可得出![]() .假设在数列
.假设在数列![]() 中存在三项
中存在三项![]() ,
,![]() ,
,![]() (其中
(其中![]() ,
,![]() ,
,![]() 成等差数列)成等比数列,则
成等差数列)成等比数列,则![]() ,推导出故
,推导出故![]() ,这与题设矛盾,所以在数列
,这与题设矛盾,所以在数列![]() 中不存在三项
中不存在三项![]() ,
,![]() ,
,![]() (其中
(其中![]() ,
,![]() ,
,![]() 成等差数列)成等比数列.
成等差数列)成等比数列.
(1)∵![]() 为“6关联数列”,
为“6关联数列”,
∴![]() 前6项为等差数列,从第5项起为等比数列.
前6项为等差数列,从第5项起为等比数列.
∴![]() ,
,![]() ,且
,且![]() .
.
即![]() ,解得
,解得![]() .
.
∴![]() .
.
(2)由(1)得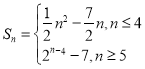 .
.
![]() :
:![]() ,
,
![]() :
:![]() ,
,
![]() :
:![]() ,
,
可见数列![]() 的最小项为
的最小项为![]() .
.
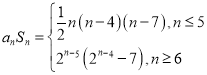 ,
,
由列举法知:当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() (
(![]() ),
),
设![]() ,则
,则![]() ,
,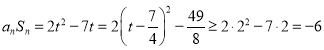 .
.
(3)由(1)可知,当![]() 时,
时,![]() ,
,
因为:![]() ,
,![]() .
.
故:![]() .
.
假设在数列![]() 中存在三项
中存在三项![]() ,
,![]() ,
,![]() (其中
(其中![]() ,
,![]() ,
,![]() 成等差数列)成等比数列,
成等差数列)成等比数列,
则:![]() ,即:
,即: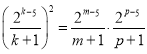 ,
,
即 (*)
(*)
因为![]() ,
,![]() ,
,![]() 成等差数列,所以
成等差数列,所以![]() ,
,
(*)式可以化简为![]() ,
,
即:![]() ,故
,故![]() ,这与题设矛盾.
,这与题设矛盾.
所以在数列![]() 中不存在三项
中不存在三项![]() ,
,![]() ,
,![]() (其中
(其中![]() ,
,![]() ,
,![]() 成等差数列)成等比数列.
成等差数列)成等比数列.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目