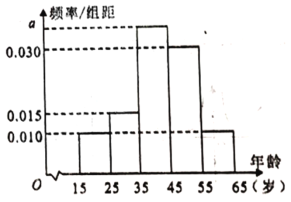
题目内容
【题目】设![]() 是定义在R上的两个函数,
是定义在R上的两个函数,![]() 满足
满足![]() ,
,![]() 满足
满足![]() ,且当
,且当![]() 时,
时,![]() ,
,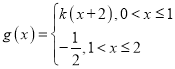 .若在区间
.若在区间![]() 上,关于
上,关于![]() 的方程
的方程![]() 有8个不同的实数根,则k的取值范围是______
有8个不同的实数根,则k的取值范围是______
【答案】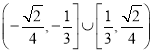
【解析】
由题可得![]() 是周期为4的函数,
是周期为4的函数,![]() 是周期为2的函数,转化方程有8个不同的实数根为
是周期为2的函数,转化方程有8个不同的实数根为![]() 与
与![]() 在
在![]() 内有8个交点,利用函数图像求解即可
内有8个交点,利用函数图像求解即可
由题,![]() ,所以
,所以![]() 的周期为
的周期为![]() ;
;
因为![]() ,则
,则![]() 的周期为2;
的周期为2;
当![]() 时,
时,![]() ,则
,则![]() 的图像为以
的图像为以![]() 为圆心,半径为1的在
为圆心,半径为1的在![]() 轴上方的半圆;由
轴上方的半圆;由![]() ,则当
,则当![]() 时,是以
时,是以![]() 为圆心, 半径为1的在
为圆心, 半径为1的在![]() 轴下方的半圆,
轴下方的半圆,
由周期性画出部分图像,如图所示,即![]() 时与
时与![]() 在
在![]() 内有2个交点,
内有2个交点,
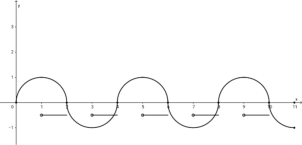
因为关于![]() 的方程
的方程![]() 有8个不同的实数根,则
有8个不同的实数根,则![]() 时与
时与![]() 在
在![]() 内需有6个交点,则
内需有6个交点,则
①令![]() 与圆
与圆![]() 相切,此时有一个交点,则
相切,此时有一个交点,则![]() ,则
,则![]() (与上半圆相切)或
(与上半圆相切)或![]() (与下半圆相切);
(与下半圆相切);
②令![]() 过
过![]() ,此时有2个交点,则
,此时有2个交点,则![]() ;令
;令![]() 过
过![]() ,此时有2个交点,则
,此时有2个交点,则![]() ;
;
假设在![]() 时有2个交点,即
时有2个交点,即![]() 与圆
与圆![]() 的上半圆有2个交点,则
的上半圆有2个交点,则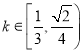 ,由函数的周期性,则在
,由函数的周期性,则在![]() 内有6个交点;
内有6个交点;
当![]() 时,图像为圆
时,图像为圆![]() 的下半圆向右平移2个单位得到,则当
的下半圆向右平移2个单位得到,则当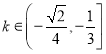 时,
时,![]() 与圆
与圆![]() 的下半圆有2个交点,由
的下半圆有2个交点,由![]() 的周期为2,则当
的周期为2,则当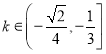 时,与
时,与![]() 也有2个交点,同理,则在
也有2个交点,同理,则在![]() 内有6个交点;
内有6个交点;
综上,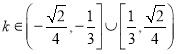
故答案为: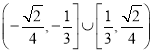

练习册系列答案
相关题目