题目内容
设函数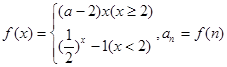 ,若数列
,若数列 是单调递减数列,则实数a的取值范围为( )
是单调递减数列,则实数a的取值范围为( )
A.(- ,2) ,2) | B.(- , , |
C.(- , , ) ) | D. |
B
解析试题分析:数列{an}是单调递减数列,即有a1>a2>a3>…>an>an+1>…,
也即f(1)>f(2)>f(3)>…,
所以,函数f(x)在x∈N+上是减函数,
故有 解得a<
解得a< .
.
所以,实数a的取值范围是(-∞, .故选B.
.故选B.
考点:一次函数、对数函数的性质,分段函数的单调性,数列的单调性。
点评:中档题,本题看似复杂,事实上,注意到数列是特殊的函数,利用函数的单调性即可得解。

练习册系列答案
相关题目
在数列 中,
中, ,且
,且 ,
, ,若数列
,若数列 满足
满足 ,则数列
,则数列 是( )
是( )
| A.递增数列 | B.递减数列 | C.常数列 | D.摆动数列 |
已知数列 满足
满足 ,且
,且 是函数
是函数 的两个零点,则
的两个零点,则 等于( )
等于( )
| A.24 | B.32 | C.48 | D.64 |
等差数列 中,
中, 分别是下表第一、二、三行中的某一个数,且
分别是下表第一、二、三行中的某一个数,且 中的任何两个数不在下表的同一列.
中的任何两个数不在下表的同一列.
则 的值为( )
的值为( )
| A.18 | B.15 | C.12 | D.20 |
已知数列 的通项公式为
的通项公式为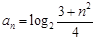 ,那么
,那么 是这个数列的( )
是这个数列的( )
| A.第3项 | B.第4项 | C.第5项 | D.第6项 |
数列 的前
的前 项和为
项和为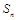 ,若
,若 ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
已知函数 数列
数列 满足
满足 是递减数列,则实数a的取值范围是
是递减数列,则实数a的取值范围是
A. | B. | C.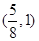 | D. |
在数列 中,
中, ,
, ,
, ,则
,则 的值是 ( )
的值是 ( )
A. | B. | C. | D. 19 |
已知定义在 上的函数
上的函数 满足
满足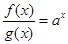 ,且
,且 ,
,  ,若有穷数列
,若有穷数列 (
( )的前
)的前 项和等于
项和等于 ,则n等于
,则n等于
| A.4 | B.5 | C.6 | D.7 |