题目内容
已知
=
，则
+
+…+
=（ ）
A． | B． | C． | D． |
D
解析试题分析：由题意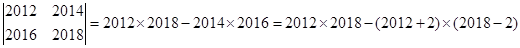
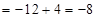，根据相同方法，每项都是
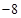，总共的项数为
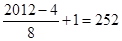，则最终的值为
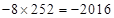，故选D.
考点：1.对新概念的理解；2.数列的通项公式与项数的应用.
练习册系列答案
阅读快车系列答案
相关题目
已知数列{an}满足an=n·pn（n∈N+，0< p<l），下面说法正确的是（ ）
①当p=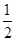
时，数列{an}为递减数列；②当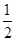<p<l时，数列{an}不一定有最大项；
③当0<p<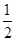时，数列{an}为递减数列；
④当
为正整数时，数列{an}必有两项相等的最大项
| A．①② | B．③④ | C．②④ | D．②③ |
在数列
中，
，且
，
，若数列
满足
，则数列是（ ）
| A．递增数列 | B．递减数列 | C．常数列 | D．摆动数列 |
已知数列
满足
，且
是函数
的两个零点，则
等于（ ）
| A．24 | B．32 | C．48 | D．64 |
等差数列
中，
分别是下表第一、二、三行中的某一个数，且中的任何两个数不在下表的同一列.
则
的值为（ ）
| A．18 | B．15 | C．12 | D．20 |
在数列
中，
，
，
，则
的值是 ( )
A． | B． | C． | D． 19 |
在数列
中，
，则
＝( )
A． |
B． |
C． |
D． |
若数列{an}满足a1=2且an+an-1=2n+2n-1,Sn为数列{an}的前n项和,则log2(S2012+2)等于( )
| A．2013 | B．2012 | C．2011 | D．2010 |
已知正项数列{an}满足a1＝1，(n＋2)an＋12－(n＋1)
＋anan＋1＝0，则它的通项公式为( )．
A．an＝ | B．an＝ |
C．an＝ | D．an＝n |