题目内容
如图,四棱锥P-ABCD中,底面ABCD为正方形,DA⊥面ABP,AB=1,PA=2,∠PAB=60°.
(1)求证:平面PBC⊥面PDC
(2)设E为PC上一点,若二面角B-EA-P的余弦值为- ,求三棱锥E-PAB的体积.
,求三棱锥E-PAB的体积.
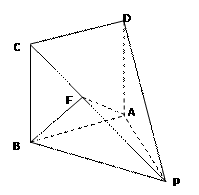
(1)求证:平面PBC⊥面PDC
(2)设E为PC上一点,若二面角B-EA-P的余弦值为-
 ,求三棱锥E-PAB的体积.
,求三棱锥E-PAB的体积.
(1)见解析
(2)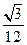
(2)
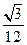
(1)∵AB=1,PA=2,∠PAB=60°,∴在△PAB中,由余弦定理得
PB2=PA2+AB2-2AB·PAcos600=4+1-2×1×2×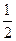 =3
=3
∴PA2=PB2+AB2,即AB⊥PB
∵DA⊥面ABP,CB∥DA
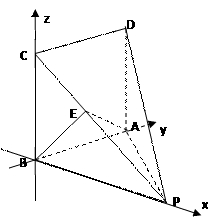
∴CB⊥面ABP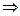 CB⊥AB ,∴AB⊥面PBC
CB⊥AB ,∴AB⊥面PBC
又DC∥AB,∴DC∥面PBC
∵DC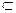 面PDC,∴平面PBC⊥面PDC
面PDC,∴平面PBC⊥面PDC
(2)如图建立空间直角坐标系
则A(0,1,0),P(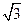 ,0,0),C(0,0,1)
,0,0),C(0,0,1)
设E(x,y,z),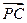 =
= 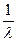
 (0<
(0<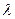 <1)
<1)
则(-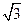 ,0,1)=
,0,1)=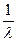 (x-
(x-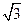 ,y,z)
,y,z)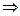 x=
x=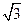 (1-
(1-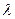 ),y=0,z=
),y=0,z=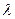
设面ABE的法向量为n=(a,b,c),则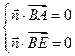
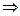
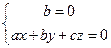
令c=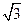
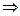
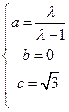
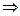 n=(
n=(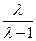 ,0,
,0,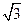 )
)
同理可求平面PAE的法向量为m=(1,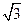 ,
,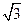 )
)
∵cos<n,m>=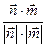 =
=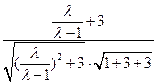 =
=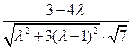 =
=
∴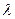 =
=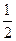 或
或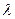 =1(舍去)
=1(舍去)
∴E(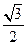 ,0,
,0,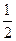 )为PC的中点,其竖坐标即为点E到底面PAB的距离
)为PC的中点,其竖坐标即为点E到底面PAB的距离
∴VE-PAB=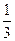 ×
×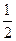 ×1×
×1×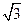 ×
×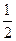 =
=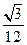
PB2=PA2+AB2-2AB·PAcos600=4+1-2×1×2×
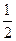 =3
=3∴PA2=PB2+AB2,即AB⊥PB
∵DA⊥面ABP,CB∥DA
∴CB⊥面ABP
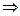 CB⊥AB ,∴AB⊥面PBC
CB⊥AB ,∴AB⊥面PBC又DC∥AB,∴DC∥面PBC
∵DC
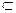 面PDC,∴平面PBC⊥面PDC
面PDC,∴平面PBC⊥面PDC(2)如图建立空间直角坐标系

则A(0,1,0),P(
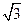 ,0,0),C(0,0,1)
,0,0),C(0,0,1)设E(x,y,z),
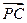 =
= 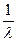
 (0<
(0<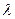 <1)
<1)则(-
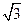 ,0,1)=
,0,1)=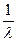 (x-
(x-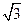 ,y,z)
,y,z)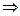 x=
x=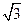 (1-
(1-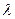 ),y=0,z=
),y=0,z=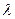
设面ABE的法向量为n=(a,b,c),则
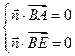
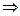
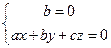
令c=
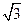
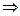
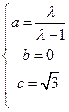
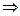 n=(
n=(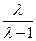 ,0,
,0,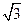 )
)同理可求平面PAE的法向量为m=(1,
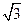 ,
,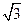 )
)∵cos<n,m>=
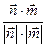 =
=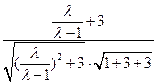 =
=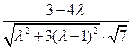 =
=
∴
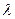 =
=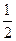 或
或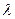 =1(舍去)
=1(舍去)∴E(
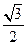 ,0,
,0,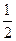 )为PC的中点,其竖坐标即为点E到底面PAB的距离
)为PC的中点,其竖坐标即为点E到底面PAB的距离∴VE-PAB=
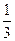 ×
×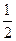 ×1×
×1×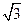 ×
×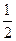 =
=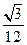

练习册系列答案
相关题目
 ,
, ,
, ,
, .又
.又 ,
, ,
, ,直线
,直线 与直线
与直线 所成的角为60°.
所成的角为60°. ;
; 的体积.
的体积.

 ,
, ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD 平面BDC(如图乙),设点E,F分别为棱AC,AD的中点.
平面BDC(如图乙),设点E,F分别为棱AC,AD的中点.
 ,求三棱锥A-BFE的体积.
,求三棱锥A-BFE的体积. 是母线
是母线 的中点,
的中点, 是底面圆的直径,半径
是底面圆的直径,半径 与母线
与母线 所成的角的大小等于
所成的角的大小等于 .
.
 与
与 所成的角;
所成的角;




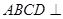 平面
平面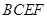 ,且四边形
,且四边形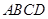 为矩形,四边形
为矩形,四边形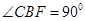 ,
,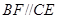 ,
,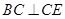 ,
,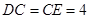 ,
,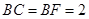 .
.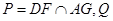 是直线
是直线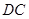 上的动点,判断并证明直线
上的动点,判断并证明直线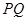 与直线
与直线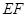 的位置关系.
的位置关系. 的体积..
的体积..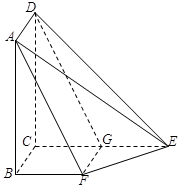
 ,E为侧棱PC的中点,则PA与BE所成的角为__________.
,E为侧棱PC的中点,则PA与BE所成的角为__________.
