题目内容
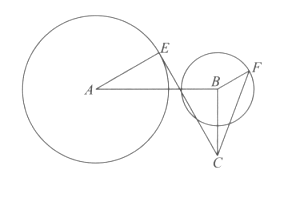
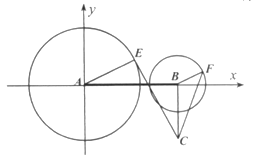
【题目】如图,已知AB⊥BC,AB=![]() BC=
BC=![]() a,a∈[1,3],圆A是以A为圆心、半径为2的圆,圆B是以B为圆心、半径为1的圆,设点E、F分别为圆A、圆B上的动点,
a,a∈[1,3],圆A是以A为圆心、半径为2的圆,圆B是以B为圆心、半径为1的圆,设点E、F分别为圆A、圆B上的动点, ![]() ∥
∥![]() (且
(且![]() 与
与![]() 同向),设∠BAE=θ(θ∈[0,π]).
同向),设∠BAE=θ(θ∈[0,π]).
(I)当a= ![]() ,且θ=
,且θ=![]() 时,求
时,求![]() 的值;
的值;
(Ⅱ)用a,θ表示出![]() ,并给出一组a,θ的值,使得
,并给出一组a,θ的值,使得![]() 最小.
最小.
【答案】(I)![]() . (II)
. (II)![]() .
.
【解析】试题分析:(Ⅰ)建立平面直角坐标系,根据向量的数量积公式计算即可,
(Ⅱ)设![]() 利用坐标计算得到关于
利用坐标计算得到关于![]() 的三角函数,利用三角函数的性质求出最值.
的三角函数,利用三角函数的性质求出最值.
试题解析:(I)如图,以点A为原点,AB所在直线为x轴,与AB垂直的直线为y轴建立平面直角坐标系.
则![]() ,
,
![]() .
.
(II)![]() ,
,
![]()
![]()
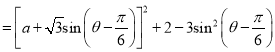
因为![]() ,所以
,所以![]() ,
,
以a为变量的二次函数的对称轴
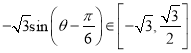 .
.
因为![]() ,所以当
,所以当![]() 时,
时, ![]() 的最小值为
的最小值为![]() ,
,
又![]() ,所以
,所以![]() 的最小值为
的最小值为![]() ,此时
,此时![]() .
.
所以,当![]() ,
, ![]() 时,
时, ![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目