题目内容
【题目】已知a>0,b>0,且 ![]() 的最小值为t.
的最小值为t.
(1)求实数t的值;
(2)解关于x的不等式:|2x+1|+|2x﹣1|<t.
【答案】
(1)解:∵已知a>0,b>0,且 ![]() ≥2
≥2 ![]() +2
+2 ![]()
≥2 ![]() =4,当且仅当a=b=1时,取等号,
=4,当且仅当a=b=1时,取等号,
故t=4
(2)解:∵|2x+1|+|2x﹣1|<t=4,∴ 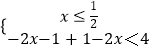 ①,
①,
或 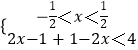 ②,或
②,或 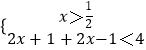 ③.
③.
解①求得﹣1<x≤﹣ ![]() ;解②求得﹣
;解②求得﹣ ![]() <x<
<x< ![]() ;解③求得
;解③求得 ![]() ≤x<1,
≤x<1,
综上可得,原不等式的解集为(﹣1,1)
【解析】(1)利用基本不等式求得 ![]() 的最小值,再根据
的最小值,再根据 ![]() 的最小值为t,求得t的值.(2)把要解的不等式等价转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.
的最小值为t,求得t的值.(2)把要解的不等式等价转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.
【考点精析】掌握基本不等式和绝对值不等式的解法是解答本题的根本,需要知道基本不等式:![]()
![]() ,(当且仅当
,(当且仅当![]() 时取到等号);变形公式:
时取到等号);变形公式:![]()
![]() ;含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.
;含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.

练习册系列答案
相关题目
【题目】某地区2007年至2013年农村居民家庭人均纯收入y(单位:千元)的数据如表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2014 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为: ![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.