题目内容
已知函数
则函数零点个数为 ( )
| A．1 | B．2 | C．3 | D．4 |
C.
解析试题分析：因为当x<0时,-x>0,所以f(-x)=-x(-x-4)=x(x+4)=f(x),所以f(x)为偶函数，因为当x>0时，f(x)有一个零点x=4,所以x<0时，f(x)也有一个零点-4,并且f(0)=0,所以还有一个零点x=0,因而f(x)有三个零点..
考点：分段函数的奇偶性，函数零点与函数方程的解关系.
点评：根据函数零点与对应的方程的根的关系，可分别求出x>0和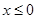
时,f(x)=0的根的个数，从而可得函数零点的个数.
练习册系列答案
相关题目
函数
的定义域为{0,1,2,3}，那么其值域为( )
A． | B．{0,1,2,3} |
C． | D． |
若定义运算
（
*b）=
则函数（
）的值域是（ ）
| A．（0，1 ] | B．[1，+∞) | C．（0．＋∞） | D．（-∞，+∞） |
f (x)＝
(n∈Z)是偶函数，且y＝f(x)在(0，＋∞)上是减函数，则n＝( ).
| A．1 | B．2 | C．1或2 | D．3 |
设方程
的实根为
，方程
的实根为
，函数
则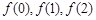
的大小关系是（ ）
A． | B． |
C． | D． |
函数
的定义域为（ ）
| A．[1，3] | B． | C．（1，3） | D． |
的定义域为开区间
，导函数
在
下图是函数f(x)的图象，它与x轴有4个不同的公共点．给出下列四个区间之中，存在不能用二分法求出的零点，该零点所在的区间是( )
| A．[－2.1，－1] | B．[4.1,5] |
| C．[1.9,2.3] | D．[5,6.1] |
、
分别是定义在R上的奇函数和偶函数，当
时，
，且
，则不等式
0的解集是（ ）
